
【题目】在平面直角坐标系中,曲线C1的参数方程为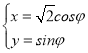 (
(![]() 为参数),以坐标原点O为极点,x轴的正半轴为极轴建立极坐标系,直线l的极坐标方程为
为参数),以坐标原点O为极点,x轴的正半轴为极轴建立极坐标系,直线l的极坐标方程为![]() ,曲线C2的极坐标方程为ρ=2sinθ.
,曲线C2的极坐标方程为ρ=2sinθ.
(1)探究直线l与曲线C2的位置关系,并说明理由;
(2)若曲线C3的极坐标方程为![]() ,且曲线C3与曲线C1、C2分别交于M、N两点,求|OM|2|ON|2的取值范围.
,且曲线C3与曲线C1、C2分别交于M、N两点,求|OM|2|ON|2的取值范围.
【答案】(1)相离,理由见解析;(2)![]()
【解析】
(1)将直线![]() 和曲线
和曲线![]() 都化成直角坐标方程后,用圆心到直线的距离与半径比较大小可得; (2)用曲线
都化成直角坐标方程后,用圆心到直线的距离与半径比较大小可得; (2)用曲线![]() 和
和![]() 的极坐标方程联立,用极径的几何意义可求解.
的极坐标方程联立,用极径的几何意义可求解.
(1)由题意得ρ2=2ρsinθ,
令y=ρsinθ,x2+y2=ρ2,得曲线C2的直角坐标方程为x2+y2﹣2y=0,即x2+(y﹣1)2=1,
由直线l:ρcos(θ![]() )=2
)=2![]() 得ρcosθ﹣ρsinθ=4,
得ρcosθ﹣ρsinθ=4,
所以直线l的直角坐标方程为x﹣y﹣4=0,
因为圆心(0,1)到直线l的距离为![]() 1,
1,
所以直线l与曲线C2相离.
(2)由题意得曲线C1的普通方程为![]() 2=1,
2=1,
故其极坐标方程为![]() ρ2sin2θ=1,
ρ2sin2θ=1,
则|OM|2![]() ,|ON|2=4sin2α,
,|ON|2=4sin2α,
即|OM|2|OB|2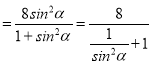 ,
,
因为0<α![]() ,所以0<sinα<1,
,所以0<sinα<1,
所以|OM|2|ON|2∈(0,4),即|OM|2|ON|2的取值范围是(0,4)


科目:高中数学 来源: 题型:
【题目】如图,矩形![]() 所在的平面和平面
所在的平面和平面![]() 互相垂直,等腰梯形
互相垂直,等腰梯形![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 分别为
分别为![]() ,
,![]() 的中点,
的中点,![]() 为底面
为底面![]() 的重心.
的重心.
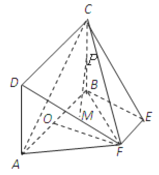
(1)求证:![]() 平面
平面![]() ;
;
(2)求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某包子店每天早晨会提前做好若干笼包子,以保证当天及时供应,每卖出一笼包子的利润为40元,当天未卖出的包子作废料处理, 每笼亏损20元.该包子店记录了60天包子的日需求量![]() (单位:笼,
(单位:笼,![]() ),整理得到如图所示的条形图,以这60天各需求量的频率代替相应的概率.
),整理得到如图所示的条形图,以这60天各需求量的频率代替相应的概率.
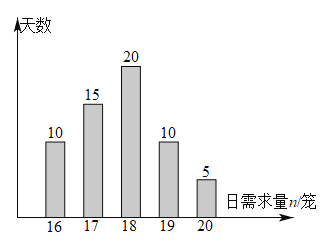
(1)设![]() 为一天的包子需求量,求
为一天的包子需求量,求![]() 的数学期望.
的数学期望.
(2)若该包子店想保证![]() 以上的天数能够足量供应,则每天至少要做多少笼包子?
以上的天数能够足量供应,则每天至少要做多少笼包子?
(3)为了减少浪费,该包子店一天只做18笼包子,设![]() 为当天的利润(单位:元),求
为当天的利润(单位:元),求![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工厂生产的30个零件编号为01,02,…,19,30,现利用如下随机数表从中抽取5个进行检测. 若从表中第1行第5列的数字开始,从左往右依次读取数字,则抽取的第5个零件编号为( )
34 57 07 86 36 04 68 96 08 23 23 45 78 89 07 84 42 12 53 31 25 30 07 32 86 |
32 21 18 34 29 78 64 54 07 32 52 42 06 44 38 12 23 43 56 77 35 78 90 56 42 |
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}的前n项和为Sn,2Sn+2n=an+1﹣2,a2=8,其中n∈N*.
(1)记bn=an+1,求证:{bn}是等比数列;
(2)设![]() 为数列{cn}的前n项和,若不等式k>Tn对任意的n∈N*恒成立,求实数k的取值范围.
为数列{cn}的前n项和,若不等式k>Tn对任意的n∈N*恒成立,求实数k的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我国是世界上严重缺水的国家,城市缺水问题尤为突出,某市为了鼓励居民节约用水,计划在本市试行居民生活用水定额管理,即确定一个合理的居民月用水量标准:(单位:吨),用水量不超过![]() 的部分按平价收费,超过
的部分按平价收费,超过![]() 的部分按议价收费,为了了解全市市民用用水量分布情况,通过袖样,获得了100位居民某年的月用水量(单位:吨),将数据按照
的部分按议价收费,为了了解全市市民用用水量分布情况,通过袖样,获得了100位居民某年的月用水量(单位:吨),将数据按照![]() ,
,![]() ……
……![]() 分成9组,制成了如图所示的频率分布直方图.
分成9组,制成了如图所示的频率分布直方图.

(1)求频率分布直方图中![]() 的值,并估计该市市民月用水量的中位数;
的值,并估计该市市民月用水量的中位数;
(2)若该市政府希望使85%的居民每月的用水量不超过标准![]() (吨),估计
(吨),估计![]() 的值,并说明理由.
的值,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com