
【题目】设a∈R,函数f(x)=x|x-a|-a.
(1) 若f(x)为奇函数,求a的值;
(2) 若对任意的x∈[2,3],f(x)≥0恒成立,求a的取值范围;
(3) 当a>4时,求函数y=f(f(x)+a)零点的个数.
【答案】(1)0(2)![]() (3)见解析
(3)见解析
【解析】
解:(1) 若f(x)为奇函数,则f(-x)=-f(x).令x=0,得f(0)=-f(0),
即f(0)=0,所以a=0,此时f(x)=x|x|为奇函数.
(2) 因为对任意的x∈[2,3],f(x)≥0恒成立,所以f(x)min≥0.
当a≤0时,对任意的x∈[2,3],f(x)=x![]() -a≥0恒成立,所以a≤0;
-a≥0恒成立,所以a≤0;
当a>0时,易得f(x)=![]() 在
在![]() 上是单调增函数,在
上是单调增函数,在![]() 上是单调减函数,在
上是单调减函数,在![]() 上是单调增函数,
上是单调增函数,
当0<a<2时,f(x)min=f(2)=2(2-a)-a≥0,解得a≤![]() ,所以a≤
,所以a≤![]() ;
;
当2≤a≤3时,f(x)min=f(a)=-a≥0,解得a≤0,所以a不存在;
当a>3时,f(x)min=min![]() =min
=min![]() ≥0,解得a≥
≥0,解得a≥![]() ,
,
所以a≥![]() .
.
综上,得a≤![]() 或a≥
或a≥![]() .
.
(3) 设y=f(f(x)+a),令t=f(x)+a=x![]() ,则y=f(t)=t
,则y=f(t)=t![]() -a,a>4,
-a,a>4,
第一步,令f(t)=0t![]() =a,
=a,
所以,当t<a时,t2-at+a=0,
判别式Δ=a(a-4)>0,
解得t1=![]() ,t2=
,t2=![]() ;
;
当t≥a时,由f(t)=0,得t(t-a)=a,
解得t3=![]() ;
;
第二步,易得0<t1<![]() <t2<a<t3,且a<
<t2<a<t3,且a<![]() ,
,
① 若x![]() =t1,其中0<t1<
=t1,其中0<t1<![]() ,
,
当x<a时,x2-ax+t1=0,记p(x)=x2-ax+t1,因为对称轴x=![]() <a,
<a,
p(a)=t1>0,且Δ1=a2-4t1>0,所以方程t2-at+t1=0有2个不同的实根;
当x≥a时,x2-ax-t1=0,记q(x)=x2-ax-t1,因为对称轴x=![]() <a,
<a,
q(a)=-t1<0,且Δ2=a2+4t1>0,所以方程x2-ax-t1=0有1个实根,
从而方程x![]() =t1有3个不同的实根;
=t1有3个不同的实根;
② 若x![]() =t2,其中0<t2<
=t2,其中0<t2<![]() ,由①知,方程x
,由①知,方程x![]() =t2有3个不同的实根;
=t2有3个不同的实根;
③ 若x![]() =t3,
=t3,
当x>a时,x2-ax-t3=0,记r(x)=x2-ax-t3,因为对称轴x=![]() <a,
<a,
r(a)=-t3<0,且Δ3=a2+4t3>0,所以方程x2-ax-t3=0有1个实根;
当x≤a时,x2-ax+t3=0,记s(x)=x2-ax-t3,因为对称轴x=![]() <a,
<a,
s(a)=t3>0,且Δ3=a2-4t3,a2-4t3>0a3-4a2-16<0,
记m(a)=a3-4a2-16,则m′(a)=a(3a-8)>0,
故m(a)为(4,+∞)上的增函数,且m(4)=-16<0,m(5)=9>0,
所以m(a)=0有唯一解,不妨记为a0,且a0∈(4,5).
若4<a<a0,即Δ3<0,方程x2-ax+t3=0有0个实根;
若a=a0,即Δ3=0,方程x2-ax+t3=0有1个实根;
若a>a0,即Δ3>0,方程x2-ax+t3=0有2个实根.
所以,当4<a<a0时,方程x![]() =t3有1个实根;
=t3有1个实根;
当a=a0时,方程x![]() =t3有2个实根;
=t3有2个实根;
当a>a0时,方程x![]() =t3有3个实根.
=t3有3个实根.
综上,当4<a<a0时,函数y=f![]() 的零点个数为7;
的零点个数为7;
当a=a0时,函数y=f![]() 的零点个数为8;
的零点个数为8;
当a>a0时,函数y=f![]() 的零点个数为9.
的零点个数为9.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】正整数数列![]() 满足
满足![]() (p,q为常数),其中
(p,q为常数),其中![]() 为数列
为数列![]() 的前n项和.
的前n项和.
(1)若![]() ,
,![]() ,求证:
,求证:![]() 是等差数列;
是等差数列;
(2)若数列![]() 为等差数列,求p的值;
为等差数列,求p的值;
(3)证明:![]() 的充要条件是
的充要条件是![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某大学为了解学生对学校食堂服务的满意度,随机调查了50名男生和50名女生,每位学生对食堂的服务给出满意或不满意的评价,得到如图所示的列联表.经计算![]() 的观测值
的观测值![]() ,则可以推断出( )
,则可以推断出( )
满意 | 不满意 | |
男 | 30 | 20 |
女 | 40 | 10 |
| 0.100 | 0.050 | 0.010 |
| 2.706 | 3.841 | 6.635 |
A.该学校男生对食堂服务满意的概率的估计值为![]()
B.调研结果显示,该学校男生比女生对食堂服务更满意
C.有95%的把握认为男、女生对该食堂服务的评价有差异
D.有99%的把握认为男、女生对该食堂服务的评价有差异
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率e满足
的离心率e满足![]() ,右顶点为A,上顶点为B,点C(0,-2),过点C作一条与y轴不重合的直线l,直线l交椭圆E于P,Q两点,直线BP,BQ分别交x轴于点M,N;当直线l经过点A时,l的斜率为
,右顶点为A,上顶点为B,点C(0,-2),过点C作一条与y轴不重合的直线l,直线l交椭圆E于P,Q两点,直线BP,BQ分别交x轴于点M,N;当直线l经过点A时,l的斜率为![]() .
.
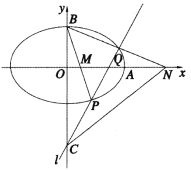
(1)求椭圆E的方程;
(2)证明:![]() 为定值.
为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱锥![]() 中,
中,![]() ,
,![]() ,O为AC的中点.
,O为AC的中点.
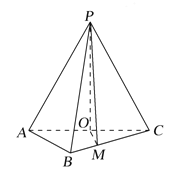
(1)证明:![]() 平面ABC;
平面ABC;
(2)若点M在棱BC上,且![]() ,求点C到平面POM的距离.
,求点C到平面POM的距离.
(3)若点M在棱BC上,且二面角![]() 为30°,求PC与平面PAM所成角的正弦值.
为30°,求PC与平面PAM所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为迎接2022年北京冬季奥运会,普及冬奥知识,某校开展了“冰雪答题王”冬奥知识竞赛活动.现从参加冬奥知识竞赛活动的学生中随机抽取了100名学生,将他们的比赛成绩(满分为100分)分为6组:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,得到如图所示的频率分布直方图.
,得到如图所示的频率分布直方图.

(1)求![]() 的值;
的值;
(2)估计这100名学生的平均成绩(同一组中的数据用该组区间的中点值为代表);
(3)在抽取的100名学生中,规定:比赛成绩不低于80分为“优秀”,比赛成绩低于80分为“非优秀”.请将下面的2×2列联表补充完整,并判断是否有99.9%的把握认为“比赛成绩是否优秀与性别有关”?
优秀 | 非优秀 | 合计 | |
男生 | 40 | ||
女生 | 50 | ||
合计 | 100 |
参考公式及数据:![]()
| 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列结论中正确的个数是( ).
①在![]() 中,若
中,若![]() ,则
,则![]() 是等腰三角形;
是等腰三角形;
②在![]() 中,若
中,若 ![]() ,则
,则![]()
③两个向量![]() ,
,![]() 共线的充要条件是存在实数
共线的充要条件是存在实数![]() ,使
,使![]()
④等差数列的前![]() 项和公式是常数项为0的二次函数.
项和公式是常数项为0的二次函数.
A.0B.1C.2D.3
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com