
���� ��1��������Բ�Ķ���ɵ�����CΪ��F1��F2Ϊ���㣬��2a=6����a=3��c=1���ɵ�b�������õ�����C�ķ��̣�
��2���ɵ�A1��-3��0����A2��3��0������M��m��n����������Բ���̣�����ֱ�ߵ�б�ʹ�ʽ�������������ɵõ�����ֵ��
��3����A��x1��y1����B��x2��y2����������֪l��б��һ����Ϊ0���ʲ�����l��x=my+2������C�ķ��̲������õ�����ϵ���Ĺ�ϵ��������ڵ�N��ʹ$\overrightarrow{OA}$+$\overrightarrow{OB}$=$\overrightarrow{ON}$����?��N�����꣨x1+x2��y1+y2��������Բ�ķ��̣���A��B����Բ�ϣ���������Բ�ķ��̣��ɵ�8x1x2+9y1y2+36=0��������m�����ɵõ���N�������ֱ��l�ķ��̣�
��� �⣺��1������P����|$\overrightarrow{P{F}_{1}}$|+|$\overrightarrow{P{F}_{2}}$|=6��
��F1��-1��0����F2��1��0���ľ���Ϊ2��6��
����Բ�Ķ���ɵ�P�Ĺ켣Ϊ��F1��F2Ϊ���㣬
��2a=6����a=3��c=1��b=$\sqrt{{a}^{2}-{c}^{2}}$=2$\sqrt{2}$��
��������C�ķ���Ϊ$\frac{{x}^{2}}{9}$+$\frac{{y}^{2}}{8}$=1��
��2��������ɵ�A1��-3��0����A2��3��0����
��M��m��n��������$\frac{{m}^{2}}{9}$+$\frac{{n}^{2}}{8}$=1��
��k1=$\frac{n}{m+3}$��k2=$\frac{n}{m-3}$��
k1k2=$\frac{{n}^{2}}{{m}^{2}-9}$=8��1-$\frac{{m}^{2}}{9}$��•$\frac{1}{{m}^{2}-9}$=-$\frac{8}{9}$��
��3����A��x1��y1����B��x2��y2����
������֪l��б��һ����Ϊ0���ʲ�����l��x=my+2��
����C�ķ��̣��������ã�8m2+9��y2+32my-40=0����Ȼ����0��
��Τ�ﶨ���У�y1+y2=-$\frac{32m}{9+8{m}^{2}}$��y1y2=-$\frac{40}{9+8{m}^{2}}$����
������ڵ�N��ʹ$\overrightarrow{OA}$+$\overrightarrow{OB}$=$\overrightarrow{ON}$������
�����Ҫ����Ϊ����N������Ϊ��x1+x2��y1+y2����
��N����Բ�ϣ���$\frac{��{x}_{1}+{x}_{2}��^{2}}{9}$+$\frac{��{y}_{1}+{y}_{2}��^{2}}{8}$=1��
�����ã�8x12+9y12��+��8x22+9y22��+16x1x2+18y1y2=72��
��A��B����Բ�ϣ���8x12+9y12=72��8x22+9y22=72��
��8x1x2+9y1y2+36=0����
��x1x2=��my1+2����my2+2��
=m2y1y2+2m��y1+y2��+4���ٴ���ڣ�
�ɵã�8m2+9��•��-$\frac{40}{9+8{m}^{2}}$��+16m•��-$\frac{32m}{9+8{m}^{2}}$��+68=0��
���m2=$\frac{7}{8}$������y1+y2=��$\frac{\sqrt{14}}{2}$��x1+x2=4-$\frac{32{m}^{2}}{9+8{m}^{2}}$=$\frac{9}{4}$��
�ʴ��ڵ�N����$\frac{\sqrt{14}}{2}$��$\frac{9}{4}$����ʹ$\overrightarrow{OA}$+$\overrightarrow{OB}$=$\overrightarrow{ON}$��
��ʱֱ��l�ķ���Ϊx=��$\frac{\sqrt{14}}{4}$y+2��
���� ���⿼������Բ�Ķ���ͱ����̼������ʡ�ֱ������Բ�ཻ����ת��Ϊ���������õ�����ϵ���Ĺ�ϵ�����������㡢�����ľ��빫ʽ�Ȼ���֪ʶ��������ܣ������˷������۵�˼�뷽�����������������������



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
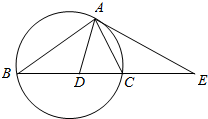 ��ͼ����ABC�����Բ������AE��BC���ӳ����ཻ�ڵ�E����BAC��ƽ������BC�ཻ�ڵ�D����֤��
��ͼ����ABC�����Բ������AE��BC���ӳ����ཻ�ڵ�E����BAC��ƽ������BC�ཻ�ڵ�D����֤���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��1��0�� | B�� | ��0��1�� | C�� | ��-1��0�� | D�� | ��0��0�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | an=$\frac{{n}^{2}-n+2}{2}$ | B�� | an=$\frac{{n}^{2}-n+1}{2}$ | C�� | an=$\frac{2}{{n}^{2}-n+1}$ | D�� | an=$\frac{2}{{n}^{2}-n+2}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com