
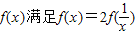 ,当x∈[1,3]时,f(x)=lnx,若在区间
,当x∈[1,3]时,f(x)=lnx,若在区间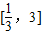 内,函数g(x)=f(x)-ax,有三个不同的零点,则实数a的取值范围是( )
内,函数g(x)=f(x)-ax,有三个不同的零点,则实数a的取值范围是( )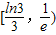
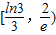
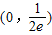
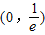
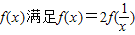 ,求出x在[
,求出x在[ ,1]上的解析式,已知在区间
,1]上的解析式,已知在区间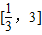 内,函数g(x)=f(x)-ax,有三个不同的零点,对g(x)进行求导,利用导数研究其单调性,从而求出a的范围;
内,函数g(x)=f(x)-ax,有三个不同的零点,对g(x)进行求导,利用导数研究其单调性,从而求出a的范围;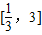 内,函数g(x)=f(x)-ax,有三个不同的零点,
内,函数g(x)=f(x)-ax,有三个不同的零点,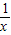 -a=
-a=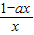 ,
,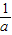 ,g(x)为减函数,
,g(x)为减函数,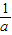 ,g(x)为增函数,
,g(x)为增函数,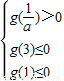 ,解得,
,解得,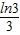 ≤a<
≤a<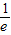 ①
① <x<1,可得1<
<x<1,可得1<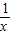 <3,
<3,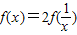 =2ln
=2ln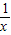 ,此时g(x)=-2lnx-ax,
,此时g(x)=-2lnx-ax, ,
,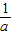 <0,g(x)为增函数
<0,g(x)为增函数 ,g(x)为减函数,
,g(x)为减函数, ,1]上有一个交点,则
,1]上有一个交点,则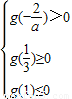 ,解得0<a≤6ln3②
,解得0<a≤6ln3②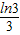 ≤a<
≤a<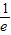 ;
; 内,函数g(x)=f(x)-ax,有三个不同的零点,
内,函数g(x)=f(x)-ax,有三个不同的零点, ≤a<
≤a<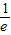 ;
;

科目:高中数学 来源:2010-2011年新疆农七七师高级中学高二下学期第一学段考试文科数学 题型:解答题
(本小题满分12分)
已知函数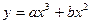 ,当x=
,当x= 1时,有极大值3。(1)求a,b的值;(2)求函数y的极小值。
1时,有极大值3。(1)求a,b的值;(2)求函数y的极小值。
查看答案和解析>>
科目:高中数学 来源:2013-2014学年四川省成都外国语学校高三(上)8月月考数学试卷(理科)(解析版) 题型:选择题
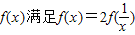 ,当x∈[1,3]时,f(x)=lnx,若在区间
,当x∈[1,3]时,f(x)=lnx,若在区间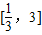 内,函数g(x)=f(x)-ax,有三个不同的零点,则实数a的取值范围是( )
内,函数g(x)=f(x)-ax,有三个不同的零点,则实数a的取值范围是( )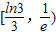
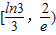
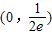
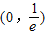
查看答案和解析>>
科目:高中数学 来源:2012年浙江省温州市高考数学一模试卷(文科)(解析版) 题型:选择题
 ,当x∈[1,3]时,f(x)=lnx,若在区间
,当x∈[1,3]时,f(x)=lnx,若在区间 内,函数g(x)=f(x)-ax,有三个不同的零点,则实数a的取值范围是( )
内,函数g(x)=f(x)-ax,有三个不同的零点,则实数a的取值范围是( )



查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com