
分析 把给出的三角不等式变形,然后逐一证得四个命题.
解答 证明:(1)sinθ•tanθ<0?sinθ≠0且cosθ<0?θ为第二或第三象限角;
(2)cosθ•tanθ<0?sinθ<0且cosθ≠0?θ为第三或第四象限角;
(3)$\frac{sinθ}{tanθ}$>0?sinθ≠0且cosθ>0?θ为第一或第四象限角;
(4)sinθ•cosθ>0?$\left\{\begin{array}{l}{sinθ>0}\\{cosθ>0}\end{array}\right.$或$\left\{\begin{array}{l}{sinθ<0}\\{cosθ<0}\end{array}\right.$?θ为第一或第三象限角.
点评 本题考查三角函数值的符号,关键是熟记三角函数的象限符号,是基础题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
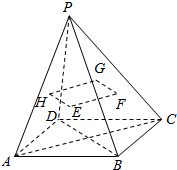 如图所示,已知四边形ABCD是平行四边形,P点是四边形ABCD所在平面外一点,连接PA、PB、PC、PD,设点E、F、G、H分别为△PAB、△PBC、△PCD、△PDA的重心.试用向量法证明E、F、G、H四点共面.
如图所示,已知四边形ABCD是平行四边形,P点是四边形ABCD所在平面外一点,连接PA、PB、PC、PD,设点E、F、G、H分别为△PAB、△PBC、△PCD、△PDA的重心.试用向量法证明E、F、G、H四点共面.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 24种 | B. | 30种 | C. | 36种 | D. | 34种 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源:2016-2017学年湖南益阳市高二9月月考数学(文)试卷(解析版) 题型:选择题
已知等差数列{an}的前n项和为Sn,a5=5,S5=15,则数列{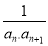 }的前100项和为
}的前100项和为
A.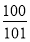 B.
B.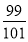 C.
C.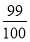 D.
D.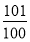
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com