
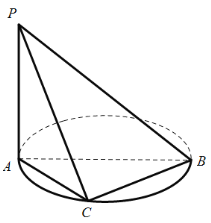
【题目】如图,AB是圆O的直径,C是圆上的点,平面PAC⊥平面ABC,PA⊥AB.
(1)求证:PA⊥平面ABC;
(2)若PA=AC=2,求点A到平面PBC的距离.
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】关于函数![]() 有下述四个结论:
有下述四个结论:
①![]() 是偶函数;②
是偶函数;②![]() 在区间
在区间![]() 单调递减;
单调递减;
③![]() 在
在![]() 有
有![]() 个零点;④
个零点;④![]() 的最大值为
的最大值为![]() .
.
其中所有正确结论的编号是( )
A.①②④B.②④C.①④D.①③
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,离心率
,离心率![]() ,点
,点![]() 是椭圆上的一个动点,
是椭圆上的一个动点,![]() 面积的最大值是
面积的最大值是![]() .
.
(1)求椭圆的方程;
(2)若![]() 是椭圆上不重合的四点,
是椭圆上不重合的四点,![]() 与
与![]() 相交于点
相交于点![]() ,
,![]() ,且
,且![]() ,求此时直线
,求此时直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数![]() .
.
(Ⅰ)当![]() 时,求函数
时,求函数![]() 的单调区间;
的单调区间;
(Ⅱ)当![]() 时,若函数
时,若函数![]() 与函数
与函数![]() 的图像总有两个交点,设两个交点的横坐标分别为
的图像总有两个交点,设两个交点的横坐标分别为![]() ,
,![]() .
.
①求![]() 的取值范围;
的取值范围;
②求证:![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆![]() ,点
,点![]() ,点
,点![]() 是圆
是圆![]() 上的一个动点,点
上的一个动点,点![]()
![]() 分别在线段
分别在线段![]()
![]() 上,且满足
上,且满足![]() ,
,![]() .
.
(1)求点![]() 的轨迹方程;
的轨迹方程;
(2)过点![]() 作斜率为
作斜率为![]() 的直线
的直线![]() 与点
与点![]() 的轨迹相交于
的轨迹相交于![]() 两点,在
两点,在![]() 轴上是否存在点
轴上是否存在点![]() ,使得以
,使得以![]() 为邻边的平行四边形是菱形?如果存在,求出
为邻边的平行四边形是菱形?如果存在,求出![]() 的取值范围;如果不存在,说明理由.
的取值范围;如果不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 的定义域是
的定义域是![]() ,有下列四个命题,其中正确的有( )
,有下列四个命题,其中正确的有( )
A.对于![]() (
(![]() ,0),函数
,0),函数![]() 在
在![]() 上是单调增函数
上是单调增函数
B.对于![]() (0,
(0,![]() ),函数
),函数![]() 存在最小值
存在最小值
C.存在![]() (
(![]() ,0),使得对于任意
,0),使得对于任意![]() ,都有
,都有![]() 成立
成立
D.存在![]() (0,
(0,![]() ),使得函数
),使得函数![]() 有两个零点
有两个零点
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(1)求函数![]() 的单调区间;
的单调区间;
(2)设![]() ,求函数
,求函数![]() 在区间
在区间![]() 上的最小值;
上的最小值;
(3)某同学发现:总存在正实数![]() ,
,![]() ,使
,使![]() ,试问:该同学的判断是否正确?若不正确,请说明理由;若正确,请直接写出
,试问:该同学的判断是否正确?若不正确,请说明理由;若正确,请直接写出![]() 的取值范围(不需要解答过程).
的取值范围(不需要解答过程).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某人的月工资由基础工资和绩效工资组成2010年每月的基础工资为2100元、绩效工资为2000元从2011年起每月基础工资比上一年增加210元、绩效工资为上一年的![]() 照此推算,此人2019年的年薪为______万元(结果精确到
照此推算,此人2019年的年薪为______万元(结果精确到![]() )
)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com