练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】如图，三棱柱ABC-A1B1C1中，侧面BCC1B1是菱形，AC=BC=2，∠CBB1=，点A在平面BCC1B1上的投影为棱BB1的中点E．

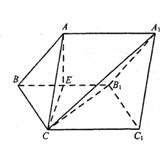
    （1）求证：四边形ACC1A1为矩形；

    （2）求二面角E-B1C-A1的平面角的余弦值．

    【答案】（1）见解析（2）

    【解析】

    （1）通过勾股定理得出，又，进而可得平面，则可得到，问题得证；

    （2）如图，以为原点，，，所在直线分别为轴，轴，轴，求出平面的法向量和平面的法向量，利用空间向量的夹角公式可得答案.

    （1）因为平面，所以，

    又因为，，，所以，

    因此，所以，

    因此平面，所以，

    从而，又四边形为平行四边形，

    则四边形为矩形；

    （2）如图，以为原点，，，所在直线分别为轴，轴，轴，所以，

    平面的法向量，设平面的法向量，

    由，

    由，

    令，即，

    所以，，

    所以，所求二面角的余弦值是.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】如图是1990年-2017年我国劳动年龄（15-64岁）人口数量及其占总人口比重情况：

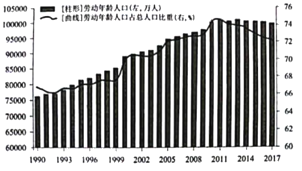
    根据图表信息，下列统计结论不正确的是（　　）

    A. 2000年我国劳动年龄人口数量及其占总人口比重的年增幅均为最大

    B. 2010年后我国人口数量开始呈现负增长态势

    C. 2013年我国劳动年龄人口数量达到峰值

    D. 我国劳动年龄人口占总人口比重极差超过

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】下列说法正确的是( )

    A.若“”为真命题，则“”为真命题

    B.命题“”的否定是“”

    C.命题“若，则”的逆否命题为真命题

    D.“”是“”的必要不充分条件

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数其中a为常数，设e为自然对数的底数.

    （1）当时，求过切点为的切线方程；

    （2）若在区间上的最大值为，求a的值；

    （3）若不等式恒成立，求a的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】为了调查一款手机的使用时间，研究人员对该款手机进行了相应的测试，将得到的数据统计如下图所示：

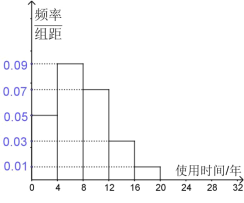
    并对不同年龄层的市民对这款手机的购买意愿作出调查，得到的数据如下表所示：

    愿意购买该款手机

    不愿意购买该款手机

    总计

    40岁以下

    600

    40岁以上

    800

    1000

    总计

    1200

    （1）根据图中的数据，试估计该款手机的平均使用时间；

    （2）请将表格中的数据补充完整，并根据表中数据，判断是否有99．9％的把握认为“愿意购买该款手机”与“市民的年龄”有关．

    参考公式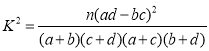：，其中．

    参考数据：

    0.100

    0.050

    0.010

    0.001

    2.706

    3.841

    6.635

    10.828

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知曲线的参数方程为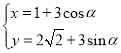，直线：，直线：.以极点为原点，极轴为轴的正半轴建立平面直角坐标系.

    （1）求直线，的直角坐标方程以及曲线的极坐标方程；

    （2）若直线与曲线交于，两点，直线与曲线交于，两点，求的面积

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】2013年华人数学家张益唐证明了孪生素数猜想的一个弱化形式．孪生素数猜想是希尔伯特在二十世纪初提出的23个数学问题之一．可以这样描述：存在无穷多个素数，使得是素数，称素数对为孪生素数．在不超过15的素数中，随机选取两个不同的数，其中能够组成孪生素数的概率是（ ）．

    A.B.C.D.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数.

    （1）求在点处的切线方程；

    （2）当时，证明：；

    （3）判断曲线与是否存在公切线，若存在，说明有几条，若不存在，说明理由.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，在正四棱锥中，，.

    （1）求证：平面；

    （2）求二面角的余弦值.

    查看答案和解析>>

    同步练习册答案