
【题目】已知函数f(x)=log4(4x+1)+kx(k∈R)是偶函数
(1)求k的值;
(2)设g(x)=log4(a2x﹣ ![]() a),若函数f(x)与g(x)的图象有且只有一个公共点,求实数a的取值范围.
a),若函数f(x)与g(x)的图象有且只有一个公共点,求实数a的取值范围.
【答案】
(1)解:∵函数f(x)=log4(4x+1)+kx(k∈R))是偶函数
∴f(﹣x)=log4(4﹣x+1)﹣kx)=log4( ![]() )﹣kx=log4(4x+1)+kx(k∈R)恒成立
)﹣kx=log4(4x+1)+kx(k∈R)恒成立
∴﹣(k+1)=k,则k= ![]()
(2)解:g(x)=log4(a2x﹣ ![]() a),
a),
函数f(x)与g(x)的图象有且只有一个公共点,即
方程f(x)=g(x)只有一个解
由已知得log4(4x+1) ![]() x=log4(a2x﹣
x=log4(a2x﹣ ![]() a),
a),
∴log4( ![]() )=log4(a2x﹣
)=log4(a2x﹣ ![]() a),
a),
方程等价于 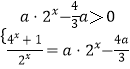 ,
,
设2x=t,t>0,则(a﹣1)t2﹣ ![]() ﹣1=0有一解
﹣1=0有一解
若a﹣1>0,设h(t)=(a﹣1)t2﹣ ![]() ﹣1,
﹣1,
∵h(0)=﹣1<0,∴恰好有一正解
∴a>1满足题意
若a﹣1=0,即a=1时,h(t)=﹣ ![]() ﹣1,由h(t)=0,得t=﹣
﹣1,由h(t)=0,得t=﹣ ![]() <0,不满足题意
<0,不满足题意
若a﹣1<0,即a<1时,由 ![]() ,得a=﹣3或a=
,得a=﹣3或a= ![]() ,
,
当a=﹣3时,t= ![]() 满足题意
满足题意
当a= ![]() 时,t=﹣2(舍去)
时,t=﹣2(舍去)
综上所述实数a的取值范围是{a|a>1或a=﹣3}
【解析】(1)根据偶函数的定义建立方程关系即可求k的值;(2)根据函数f(x)与g(x)的图象有且只有一个公共点,即可得到结论.


科目:高中数学 来源: 题型:
【题目】已知数据![]() 是上海普通职工n
是上海普通职工n![]() 个人的年收入,设n个数据的中位数为x,平均数为y,方差为z,如果再加上世界首富的年收入
个人的年收入,设n个数据的中位数为x,平均数为y,方差为z,如果再加上世界首富的年收入![]() , 则这n+1个数据中,下列说法正确的是 ( )
, 则这n+1个数据中,下列说法正确的是 ( )
A.年收入平均数大大增加,中位数一定变大,方差可能不变
B.年收入平均数大大增加,中位数可能不变,方差变大
C.年收入平均数大大增加,中位数可能不变,方差也不变
D.年收入平均数可能不变,中位数可能不变,方差可能不变
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下面茎叶图表示的是甲、乙两人在5次综合测评中的成绩(成绩为整数,满分为100),其中一个数字被污损,则乙的平均成绩不低于甲的平均成绩的概率为( ) 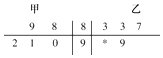
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知等差数列{an}满足:a2=3,a5﹣2a3+1=0.
(1)求{an}的通项公式;
(2)若数列{bn}满足:{bn}=(﹣1)nann(+n∈N*),求{bn}的前n项和Sn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,平行六面体ABCD﹣A1B1C1D1中,侧棱B1B长为3,底面是边长为2的菱形,∠A1AB=120°,∠A1AD=60°,点E在棱B1B上,则AE+C1E的最小值为( )
A.![]()
B.5
C.2![]()
D.7
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆C过点(1,2)和(2,1),且圆心在直线x+y﹣4=0上.
(Ⅰ)求圆C的方程;
(Ⅱ)若一束光线l自点A(﹣3,3)发出,射到x轴上,被x轴反射到圆C上,若反射点为M(a,0),求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】统计表明,某种型号的汽车在匀速行驶中每小时的耗油量y(升)关于行驶速度x(千米/小时)的函数解析式可以表示为:y=![]() (0<x≤120).已知甲、乙两地相距100千米.
(0<x≤120).已知甲、乙两地相距100千米.
(Ⅰ)当汽车以40千米/小时的速度匀速行驶时,从甲地到乙地要耗油多少升?
(Ⅱ)当汽车以多大的速度匀速行驶时,从甲地到乙地耗油最少?最少为多少升?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,要设计一张矩形广告,该广告含有大小相等的左右两个矩形栏目(即图中阴影部分),这两栏的面积之和为18000cm2 , 四周空白的宽度为10cm,两栏之间的中缝空白的宽度为5cm. 
(1)设矩形栏目宽度为xcm,求矩形广告面积S(x)的表达式
(2)怎样确定广告的高与宽的尺寸(单位:cm),能使矩形广告面积最小?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com