
【题目】三棱柱![]() 中,
中,![]() 为
为![]() 的中点,点
的中点,点![]() 在侧棱
在侧棱![]() 上,
上,![]() 平面
平面![]() .
.
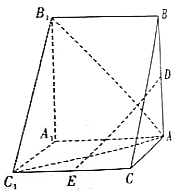
(1)证明:![]() 是
是![]() 的中点;
的中点;
(2)设![]() ,四边形
,四边形![]() 为正方形,四边形
为正方形,四边形![]() 为矩形,且异面直线
为矩形,且异面直线![]() 与
与![]() 所成的角为30°,求两面角
所成的角为30°,求两面角![]() 的余弦值.
的余弦值.
【答案】(1)见解析;(2)二面角![]() 的余弦值为
的余弦值为![]() .
.
【解析】
(1)取![]() 的中点
的中点![]() ,利用中位线得出
,利用中位线得出![]() 利用线面平行的判定,得出
利用线面平行的判定,得出![]() 平面
平面![]() ,利用面面平行的判定得出平面
,利用面面平行的判定得出平面![]() 平面
平面![]() 进而得出
进而得出![]() 而
而![]() 为
为![]() 的中点,所以
的中点,所以![]() 为
为![]() 的中点。
的中点。
(2)建立直角坐标系,设![]() ,
,![]() ,利用异面直线
,利用异面直线![]() 与
与![]() 所成的角为30°,求出
所成的角为30°,求出![]() 进而求出二面角
进而求出二面角![]() 的余弦值。
的余弦值。
(1)证明:取![]() 的中点
的中点![]() ,连
,连![]() 、
、![]() ,因为
,因为![]() 为
为![]() 中点,所以
中点,所以![]() .
.
![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,![]() 平面
平面![]() .
.
又由已知![]() 平面
平面![]() ,
,
且![]() ,所以平面
,所以平面![]() 平面
平面![]() .
.
又![]() 平面
平面![]() ,所
,所![]() 平面
平面![]() .
.
而![]() 平面
平面![]() ,且平面
,且平面![]() 平面
平面![]() ,所以
,所以![]() ,而
,而![]() 为
为![]() 的中点,所以
的中点,所以![]() 为
为![]() 的中点.
的中点.
(2)由题设知:![]() 、
、![]() 、
、![]() 两两垂直,以
两两垂直,以![]() 为
为![]() 轴,
轴,![]() 为
为![]() 轴,
轴,![]() 为
为![]() 轴,建立空间直角坐标系
轴,建立空间直角坐标系![]() .
.
设![]() ,
,![]() ,则
,则![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
所以![]() ,
,![]() .因为异面直线
.因为异面直线![]() 与
与![]() 所成的角为30°,
所成的角为30°,
所以![]()
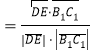
![]()
![]() ,解得:
,解得:![]() ,于是
,于是![]() .
.
设平面![]() 的法向量为
的法向量为![]() ,因为
,因为![]() ,
,![]()
所以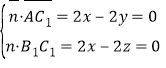 ,取
,取![]() ,则
,则![]() ,所以
,所以![]() .
.
又![]() 是平面
是平面![]() 的一个法向量,所以
的一个法向量,所以![]() ,
,
即二面角![]() 的余弦值为
的余弦值为![]() .
.


科目:高中数学 来源: 题型:
【题目】某地区不同身高![]() 的未成年男性的体重平均值
的未成年男性的体重平均值![]() 如下表:
如下表:
身高x(cm) | 60 | 70 | 80 | 90 | 100 | 110 | 120 | 130 | 140 |
体重y(kg) | 6.13 | 7.90 | 9.99 | 12.15 | 15.02 | 17.50 | 20.92 | 26.86 | 31.11 |
已知![]() 与
与![]() 之间存在很强的线性相关性,
之间存在很强的线性相关性,
(Ⅰ)据此建立![]() 与
与![]() 之间的回归方程;
之间的回归方程;
(Ⅱ)若体重超过相同身高男性体重平均值的![]() 倍为偏胖,低于
倍为偏胖,低于![]() 倍为偏瘦,那么这个地区一名身高
倍为偏瘦,那么这个地区一名身高![]() 体重为
体重为![]()
![]() 的在校男生的体重是否正常?
的在校男生的体重是否正常?
参考数据:![]()
附:对于一组数据![]() ,其回归直线
,其回归直线![]() 中的斜率和截距的最小二乘估计分别为
中的斜率和截距的最小二乘估计分别为
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 的内角
的内角![]() 、
、![]() 、
、![]() 的对边分别为
的对边分别为![]() 、
、![]() 、
、![]() ,
,![]() 为
为![]() 内一点,若分别满足下列四个条件:
内一点,若分别满足下列四个条件:
①![]() ;
;
②![]() ;
;
③![]() ;
;
④![]() ;
;
则点![]() 分别为
分别为![]() 的( )
的( )
A.外心、内心、垂心、重心B.内心、外心、垂心、重心
C.垂心、内心、重心、外心D.内心、垂心、外心、重心
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知曲线C1:y=cos x,C2:y=sin (2x+![]() ),则下面结论正确的是( )
),则下面结论正确的是( )
A. 把C1上各点的横坐标伸长到原来的2倍,纵坐标不变,再把得到的曲线向右平移![]() 个单位长度,得到曲线C2
个单位长度,得到曲线C2
B. 把C1上各点的横坐标伸长到原来的2倍,纵坐标不变,再把得到的曲线向左平移![]() 个单位长度,得到曲线C2
个单位长度,得到曲线C2
C. 把C1上各点的横坐标缩短到原来的![]() 倍,纵坐标不变,再把得到的曲线向右平移
倍,纵坐标不变,再把得到的曲线向右平移![]() 个单位长度,得到曲线C2
个单位长度,得到曲线C2
D. 把C1上各点的横坐标缩短到原来的![]() 倍,纵坐标不变,再把得到的曲线向左平移
倍,纵坐标不变,再把得到的曲线向左平移![]() 个单位长度,得到曲线C2
个单位长度,得到曲线C2
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,两铁路线垂直相交于站![]() ,若已知
,若已知![]() 千米,甲火车从
千米,甲火车从![]() 站出发,沿
站出发,沿![]() 方向以
方向以![]() 千米
千米![]() 小时的速度行驶,同时乙火车从
小时的速度行驶,同时乙火车从![]() 站出发,沿
站出发,沿![]() 方向,以
方向,以![]() 千米
千米![]() 小时的速度行驶,至
小时的速度行驶,至![]() 站即停止前行(甲车扔继续行驶)(两车的车长忽略不计).
站即停止前行(甲车扔继续行驶)(两车的车长忽略不计).
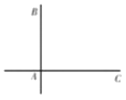
(1)求甲、乙两车的最近距离(用含![]() 的式子表示);
的式子表示);
(2)若甲、乙两车开始行驶到甲,乙两车相距最近时所用时间为![]() 小时,问
小时,问![]() 为何值时
为何值时![]() 最大?
最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设{an}是公比为 q的等比数列,且a1,a3,a2成等差数列.
(Ⅰ)求q的值;
(Ⅱ)设{bn}是以2为首项,q为公差的等差数列,其前n项和为Sn,当n≥2时,比较Sn与bn的大小,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着移动互联网的发展,与餐饮美食相关的手机APP软件层出不穷.现从某市使用A和B两款订餐软件的商家中分别随机抽取100个商家,对它们的“平均送达时间”进行统计,得到频率分布直方图如下.
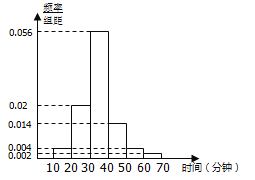
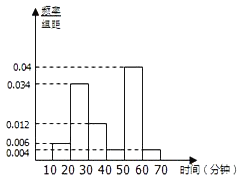
![]()
![]()
(1)已知抽取的100个使用A款订餐软件的商家中,甲商家的“平均送达时间”为18分钟。现从使用A款订餐软件的商家中“平均送达时间”不超过20分钟的商家中随机抽取3个商家进行市场调研,求甲商家被抽到的概率;
(2)试估计该市使用A款订餐软件的商家的“平均送达时间”的众数及平均数;
(3)如果以“平均送达时间”的平均数作为决策依据,从A和B两款订餐软件中选择一款订餐,你会选择哪款?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com