
【题目】已知函数![]() .
.
(1)讨论![]() 的单调性;
的单调性;
(2)若![]() ,
,![]() 是
是![]() 的两个零点,求证:
的两个零点,求证:![]() .
.
【答案】(1)f(x)的单调递增区间为![]() ,单调递减区间为
,单调递减区间为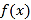 .(2)证明见解析
.(2)证明见解析
【解析】
(1)先求函数的导数![]()
![]() ,分
,分![]() 和
和![]() 两种情况讨论函数的单调性;
两种情况讨论函数的单调性;
(2)根据(1)的结果可知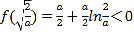 ,即
,即![]() ,利用分析法,将需要证明想不等式转化为证明
,利用分析法,将需要证明想不等式转化为证明![]() ,只需证明
,只需证明![]() ,利用函数的单调性和零点存在性定理可证明
,利用函数的单调性和零点存在性定理可证明![]() ,根据零点存在性定理和单调性证明.
,根据零点存在性定理和单调性证明.
(1)f(x)的定义域为(0,+∞),且![]() ,
,
①当a≤0时,f'(x)≤0,f(x)的单调递减区间为(0,+∞);②当a>0时,由f'(x)>0得![]() ,故f(x)的单调递增区间为
,故f(x)的单调递增区间为![]() ,
,
单调递减区间为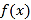 .
.
(2)∵f(x)有两个零点,∴由(1)知a>0且![]() ,∴a>2e,要证原不等式成立,只需证明
,∴a>2e,要证原不等式成立,只需证明![]() ,只需证明
,只需证明![]() ,
,
只需证明![]() .
.
一方面∵a>2e,∴![]() ,
,
∴![]() ,∴
,∴![]() ,
,
且f(x)在![]() 单调递增,故
单调递增,故![]() ;
;
另一方面,令![]() ,(x>0),
,(x>0),
则![]() ,当
,当![]() 时,g'(x)<0;当
时,g'(x)<0;当![]() 时,g'(x)>0;
时,g'(x)>0;
故![]() ,故g(x)≥0即
,故g(x)≥0即![]() 时x∈(0,+∞)恒成立,
时x∈(0,+∞)恒成立,
令![]() ,
,
则![]() ,于是
,于是![]() ,
,
而![]() ,
,
故![]() ,且f(x)在
,且f(x)在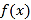 单调递减,故
单调递减,故![]() ;
;
综合上述,![]() ,即原不等式成立.
,即原不等式成立.


 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案科目:高中数学 来源: 题型:
【题目】已知王明比较喜爱打篮球,近来,他为了提高自己的投篮水平,制定了一个夏季训练计划.班主任为了了解其训练效果,开始训练前,统计了王明![]() 场比赛的得分,计算出得分数据的中位数为
场比赛的得分,计算出得分数据的中位数为![]() 分,平均得分为
分,平均得分为![]() 分,得分数据的方差为
分,得分数据的方差为![]() ,训练结束后统计了
,训练结束后统计了![]() 场比赛得分成绩茎叶图如下图:
场比赛得分成绩茎叶图如下图:
![]()
(1)求王明训练结束后统计的![]() 场比赛得分的中位数,平均得分以及方差;
场比赛得分的中位数,平均得分以及方差;
(2)若只从训练前后统计的各![]() 场比赛得分数据分析,训练计划对王明投篮水平的提高是否有帮助?
场比赛得分数据分析,训练计划对王明投篮水平的提高是否有帮助?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数u(x)=xlnx,v(x)![]() x﹣1,m∈R.
x﹣1,m∈R.
(1)令m=2,求函数h(x)![]() 的单调区间;
的单调区间;
(2)令f(x)=u(x)﹣v(x),若函数f(x)恰有两个极值点x1,x2,且满足1![]() e(e为自然对数的底数)求x1x2的最大值.
e(e为自然对数的底数)求x1x2的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某调查机构为了了解某产品年产量x(吨)对价格y(千克/吨)和利润z的影响,对近五年该产品的年产量和价格统计如下表:
x | 1 | 2 | 3 | 4 | 5 |
y | 17.0 | 16.5 | 15.5 | 13.8 | 12.2 |
(1)求y关于x的线性回归方程![]() ;
;
(2)若每吨该产品的成本为12千元,假设该产品可全部卖出,预测当年产量为多少时,年利润w取到最大值?
参考公式: 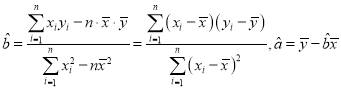
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com