
ЁОЬтФПЁПЙЋАВВПНЛЙмОжаоИФКѓЕФОЦКѓЮЅЗЈМнЪЛЛњЖЏГЕЕФааЮЊЗжГЩСНИіЕЕДЮЃКЁАОЦКѓМнГЕЁБКЭЁАзэОЦМнГЕЁБЃЌЦфХаЖЯБъзМЪЧМнЪЛШЫдБУП100КСЩ§бЊвКжаЕФОЦОЋКЌСПXКСПЫЃЌЕБ20ЁмX<80ЪБЃЌШЯЖЈЮЊОЦКѓМнГЕЃЛЕБXЁн80ЪБЃЌШЯЖЈЮЊзэОЦМнГЕЃЌжиЧьЪаЙЋАВОжНЛЭЈЙмРэВПУХдкЖдG42ИпЫйТЗЮвЪаТЗЖЮЕФвЛДЮЫцЛњРЙВщааЖЏжаЃЌвРЗЈМьВтСЫ200СОЛњЖЏГЕМнЪЛдБЕФУП100КСЩ§бЊвКжаЕФОЦОЋКЌСПЃЌОЦОЋКЌСПX(ЕЅЮЛЃККСПЫ)ЕФЭГМЦНсЙћШчЯТБэЃК
X | [0ЃЌ20) | [20ЃЌ40) | [40ЃЌ60) | [60ЃЌ80) | [80ЃЌ100) | [100ЃЌЃЋЁо) |
ШЫЪ§ | t | 1 | 1 | 1 | 1 | 1 |
вРОнЩЯЪіВФСЯЛиД№ЯТСаЮЪЬтЃК
(1)ЧѓtЕФжЕЃЛ
(2)ДгОЦКѓЮЅЗЈМнГЕЕФЫОЛњжаЫцЛњГщШЁ2ШЫЃЌЧѓет2ШЫжаКЌгазэОЦМнГЕЫОЛњЕФИХТЪЃЎ

| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПгые§ЗНЬхABCDЁЊA1B1C1D1ЕФШ§ЬѕРтABЁЂCC1ЁЂA1D1ЫљдкжБЯпЕФОрРыЯрЕШЕФЕу( )
A.гаЧвжЛга1ИіB.гаЧвжЛга2Иі
C.гаЧвжЛга3ИіD.гаЮоЪ§Иі
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊе§ЯюЕШБШЪ§Са![]() ЃЌЕШВюЪ§Са
ЃЌЕШВюЪ§Са![]() Тњзу
Тњзу![]() ЃЌЧв
ЃЌЧв![]() ЪЧ
ЪЧ![]() гы
гы![]() ЕФЕШБШжаЯю.
ЕФЕШБШжаЯю.
ЃЈ1ЃЉЧѓЪ§Са![]() ЕФЭЈЯюЙЋЪНЃЛ
ЕФЭЈЯюЙЋЪНЃЛ
ЃЈ2ЃЉЩш![]() ЃЌЧѓЪ§Са
ЃЌЧѓЪ§Са![]() ЕФЧА
ЕФЧА![]() ЯюКЭ
ЯюКЭ![]() .
.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊ![]() ,Щш
,Щш![]() ,Чв
,Чв![]() ,МЧ
,МЧ![]() ;
;
ЃЈ1ЃЉЩш![]() ,Цфжа
,Цфжа![]() ,ЪдЧѓ
,ЪдЧѓ![]() ЕФЕЅЕїЧјМф;
ЕФЕЅЕїЧјМф;
ЃЈ2ЃЉЪдХаЖЯЯв![]() ЕФаБТЪ
ЕФаБТЪ![]() гы
гы![]() ЕФДѓаЁЙиЯЕ,ВЂжЄУї;
ЕФДѓаЁЙиЯЕ,ВЂжЄУї;
ЃЈ3ЃЉжЄУїЃКЕБ![]() ЪБ,
ЪБ,![]() .
.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПИјГіЫФИіУќЬтЃКЂйШєx2Љ3x+2ЃН0ЃЌдђxЃН1ЛђxЃН2ЃЛЂкШєxЃНyЃН0ЃЌдђx2+y2ЃН0ЃЛЂлвбжЊxЃЌyЁЪNЃЌШєx+yЪЧЦцЪ§ЃЌдђxЁЂyжавЛИіЪЧЦцЪ§ЃЌвЛИіЪЧХМЪ§ЃЛЂмШєx1ЃЌx2ЪЧЗНГЬx2Љ2![]() x+2ЃН0ЕФСНИљЃЌдђx1ЃЌx2ПЩвдЪЧвЛЭждВгывЛЫЋЧњЯпЕФРыаФТЪЃЌФЧУДЃЈЁЁ ЁЁЃЉ
x+2ЃН0ЕФСНИљЃЌдђx1ЃЌx2ПЩвдЪЧвЛЭждВгывЛЫЋЧњЯпЕФРыаФТЪЃЌФЧУДЃЈЁЁ ЁЁЃЉ
A.ЂлЕФЗёУќЬтЮЊМйB.ЂйЕФФцЗёУќЬтЮЊМй
C.ЂкЕФФцУќЬтЮЊецD.ЂмЕФФцЗёУќЬтЮЊМй
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПедЫЌЪЧЮвЙњЙХДњЪ§бЇМвЁЂЬьЮФбЇМвЃЌДѓдМдкЙЋдЊ222ФъЃЌедЫЌЮЊЁЖжмїТЫуОЁЗвЛЪщзїађЪБЃЌНщЩмСЫЁАЙДЙЩдВЗНЭМЁБЃЌврГЦЁАедЫЌЯвЭМЁБЃЈвдЯвЮЊБпГЄЕУЕНЕФе§ЗНаЮгЩ4ИіШЋЕШЕФжБНЧШ§НЧаЮдйМгЩЯжаМфЕФвЛИіаЁе§ЗНаЮзщГЩЕФЃЉЃЌРрБШЁАедЫЌЯвЭМЁБЃЌПЩРрЫЦЕиЙЙдьШчЭМЫљЪОЕФЭМаЮЃЌЫќЪЧгЩ3ИіШЋЕШЕФШ§НЧаЮгыжаМфЕФвЛИіаЁЕШБпШ§НЧаЮЦДГЩЕФвЛИіДѓЕШБпШ§НЧаЮЃЌЩш![]() ЃЌдђЃЈ ЃЉ
ЃЌдђЃЈ ЃЉ
A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
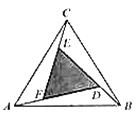
ЁОЬтФПЁПдкШчЭМЫљЪОЕФМИКЮЬхжаЃЌЫФБпаЮCDEFЮЊе§ЗНаЮЃЌЫФБпаЮABCDЮЊЬнаЮЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЦНУцABCDЃЎ
ЦНУцABCDЃЎ
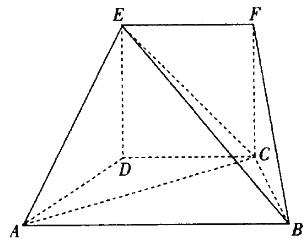
![]() ЧѓBEгыЦНУцEACЫљГЩНЧЕФе§ЯвжЕЃЛ
ЧѓBEгыЦНУцEACЫљГЩНЧЕФе§ЯвжЕЃЛ
![]() ЯпЖЮBEЩЯЪЧЗёДцдкЕуMЃЌЪЙЦНУц
ЯпЖЮBEЩЯЪЧЗёДцдкЕуMЃЌЪЙЦНУц![]() ЦНУцDFMЃПШєДцдкЃЌЧѓ
ЦНУцDFMЃПШєДцдкЃЌЧѓ![]() ЕФжЕЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
ЕФжЕЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкОиаЮABCDжаЃЌ![]() ЃЌEЮЊABЕФжаЕуЃЎНЋ
ЃЌEЮЊABЕФжаЕуЃЎНЋ![]() биDEЗелЃЌЕУЕНЫФРтзЖ
биDEЗелЃЌЕУЕНЫФРтзЖ![]() ЃЎЩш
ЃЎЩш![]() ЕФжаЕуЮЊMЃЌдкЗелЙ§ГЬжаЃЌгаЯТСаШ§ИіУќЬтЃК
ЕФжаЕуЮЊMЃЌдкЗелЙ§ГЬжаЃЌгаЯТСаШ§ИіУќЬтЃК
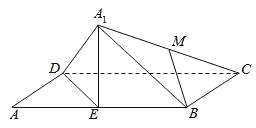
Ђйзмга![]() ЦНУц
ЦНУц![]() ЃЛ
ЃЛ
ЂкЯпЖЮBMЕФГЄЮЊЖЈжЕЃЛ
ЂлДцдкФГИіЮЛжУЃЌЪЙDEгы![]() ЫљГЩЕФНЧЮЊ90ЁуЃЎ
ЫљГЩЕФНЧЮЊ90ЁуЃЎ
Цфжае§ШЗЕФУќЬтЪЧ_______ЃЎЃЈаДГіЫљгае§ШЗУќЬтЕФађКХЃЉ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЭждВЃК![]() ЕФЫФИіЖЅЕуЮЇГЩЕФЫФБпаЮЕФУцЛ§ЮЊ
ЕФЫФИіЖЅЕуЮЇГЩЕФЫФБпаЮЕФУцЛ§ЮЊ![]() ЃЌдЕуЕНжБЯп
ЃЌдЕуЕНжБЯп![]() ЕФОрРыЮЊ
ЕФОрРыЮЊ![]() .
.
ЃЈ1ЃЉЧѓЭждВ![]() ЕФЗНГЬЃЛ
ЕФЗНГЬЃЛ
ЃЈ2ЃЉвбжЊЖЈЕу![]() ЃЌЪЧЗёДцдкЙ§
ЃЌЪЧЗёДцдкЙ§![]() ЕФжБЯп
ЕФжБЯп![]() ЃЌЪЙ
ЃЌЪЙ![]() гыЭждВ
гыЭждВ![]() НЛгк
НЛгк![]() ЃЌ
ЃЌ![]() СНЕуЃЌЧввд
СНЕуЃЌЧввд![]() ЮЊжБОЖЕФдВЙ§ЭждВ
ЮЊжБОЖЕФдВЙ§ЭждВ![]() ЕФзѓЖЅЕуЃПШєДцдкЃЌЧѓГі
ЕФзѓЖЅЕуЃПШєДцдкЃЌЧѓГі![]() ЕФЗНГЬЃКШєВЛДцдкЃЌЧыЫЕУїРэгЩ.
ЕФЗНГЬЃКШєВЛДцдкЃЌЧыЫЕУїРэгЩ.
ВщПДД№АИКЭНтЮі>>
АйЖШжТаХ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com