
分析 通过解含有绝对值的表达式可知-3≤x-y≤-1、-3≤3x-2y≤3,画出图象、计算可知C(9,12),进而计算即得结论.
解答 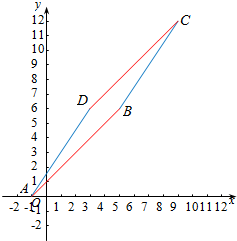 解:∵|x-y+2|≤1,
解:∵|x-y+2|≤1,
∴-3≤x-y≤-1,
∵|3x-2y|≤3,
∴-3≤3x-2y≤3,
∴联立$\left\{\begin{array}{l}{x-y=-3}\\{3x-2y=-3}\end{array}\right.$,解得$\left\{\begin{array}{l}{x=9}\\{y=12}\end{array}\right.$,即C(9,12),
∴|5x+4|的最大值为|5×9+4|=49,
故答案为:49.
点评 本题是一道简单随机规划题,涉及到含有绝对值的表达式,考查数形结合能力,注意解题方法的积累,属于中档题.


 文敬图书课时先锋系列答案
文敬图书课时先锋系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4$\sqrt{2}$ | B. | 2$\sqrt{2}$ | C. | 8 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
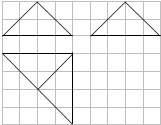
| A. | 8+12$\sqrt{2}$ | B. | 16+24$\sqrt{2}$ | C. | $\frac{1}{3}(8+12\sqrt{2})$ | D. | 4+6$\sqrt{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com