
| A. | 1 | B. | 0 | C. | π+1 | D. | 1-cos1 |
分析 由=${∫}_{0}^{\frac{π}{2}}$(2+sinx)dx,求得2+sinx的原函数,代入即可求得$f({\frac{π}{2}})$的值.
解答 解:由f(a)=$\int_0^a{({2+sinx})dx}$,则$f({\frac{π}{2}})$=${∫}_{0}^{\frac{π}{2}}$(2+sinx)dx,
=(2x-cosx)${丨}_{0}^{\frac{π}{2}}$,
=2×$\frac{π}{2}$-cos$\frac{π}{2}$-(2×0-cos0)=π+1,
∴$f({\frac{π}{2}})$=π+1,
故选C.
点评 本题考查定积分的运算,考查计算能力,属于基础题.


 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案科目:高中数学 来源: 题型:选择题
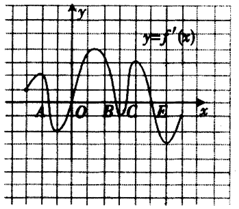 函数y=f(x)定义在区间(-3,7)上,其导函数如图所示,则函数y=f(x)在区间(-3,7)上极小值的个数是( )
函数y=f(x)定义在区间(-3,7)上,其导函数如图所示,则函数y=f(x)在区间(-3,7)上极小值的个数是( )| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (1)(2)(5)(6) | B. | (3)(6) | C. | (2)(3)(4) | D. | (6) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 如图,在直角梯形ABCD中,AB⊥AD,AB∥DC,AB=2,AD=DC=1,图中圆弧所在圆的圆心为点C,半径为$\frac{1}{2}$,且点P在图中阴影部分(包括边界)运动.若$\overrightarrow{AP}=x\overrightarrow{AB}+y\overrightarrow{BC}$,其中x,y∈R,则4x-y的最大值为( )
如图,在直角梯形ABCD中,AB⊥AD,AB∥DC,AB=2,AD=DC=1,图中圆弧所在圆的圆心为点C,半径为$\frac{1}{2}$,且点P在图中阴影部分(包括边界)运动.若$\overrightarrow{AP}=x\overrightarrow{AB}+y\overrightarrow{BC}$,其中x,y∈R,则4x-y的最大值为( )| A. | $3-\frac{{\sqrt{2}}}{4}$ | B. | $3+\frac{{\sqrt{5}}}{2}$ | C. | 2 | D. | $3+\;\frac{{\sqrt{17}}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| 甲 | 乙 | 丙 | 丁 | |
| R2 | 0.98 | 0.78 | 0.50 | 0.85 |
| A. | 甲 | B. | 乙 | C. | 丙 | D. | 丁 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | tanx | B. | sinx | C. | cosx | D. | $\frac{1}{tanx}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既非充分也非必要条件 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com