
【题目】已知数列![]() (其中第一项是
(其中第一项是![]() ,接下来的
,接下来的![]() 项是
项是![]() ,再接下来的
,再接下来的![]() 项是
项是![]() ,依此类推)的前
,依此类推)的前![]() 项和为
项和为![]() ,下列判断:
,下列判断:
①![]() 是
是![]() 的第
的第![]() 项;②存在常数
项;②存在常数![]() ,使得
,使得![]() 恒成立;③
恒成立;③![]() ;④满足不等式
;④满足不等式![]() 的正整数
的正整数![]() 的最小值是
的最小值是![]() .
.
其中正确的序号是( )
A.①③B.①④C.①③④D.②③④
【答案】B
【解析】
找出数列![]() 的规律:分母为
的规律:分母为![]() 的项有
的项有![]() 项,并将这些项排成杨辉三角形式的数阵,使得第
项,并将这些项排成杨辉三角形式的数阵,使得第![]() 有
有![]() 项,每项的分母均为
项,每项的分母均为![]() ,并计算出每行各项之和
,并计算出每行各项之和![]() ,并计算出数列
,并计算出数列![]() 的前
的前![]() 项和
项和![]() ,结合这些规律来判断各题的正误。
,结合这些规律来判断各题的正误。
由题意可知,数列![]() 的规律为:分母为
的规律为:分母为![]() 的项有
的项有![]() 项,将数列
项,将数列![]() 中的项排成杨辉三角数阵,且使得第
中的项排成杨辉三角数阵,且使得第![]() 行每项的分母为
行每项的分母为![]() ,该行有
,该行有![]() 项,如下所示:
项,如下所示:
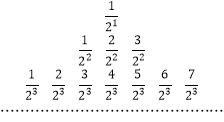
对于命题①,![]() 位于数阵第
位于数阵第![]() 行最后一项,对应于数列
行最后一项,对应于数列![]() 的项数为
的项数为
![]() ,命题①正确;
,命题①正确;
对于命题②,数阵中第![]() 行各项之和为
行各项之和为![]() ,则
,则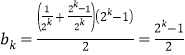 ,
,
且数列![]() 的前
的前![]() 项之和为
项之和为
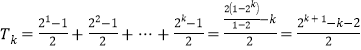 ,
,
当![]() 时,
时,![]() ,因此,不存在正数
,因此,不存在正数![]() ,使得
,使得![]() ,命题②错误;
,命题②错误;
对于命题③,易知第![]() 行最后一项位于数列
行最后一项位于数列![]() 的项数为
的项数为
![]() ,
,
第![]() 行最后一项位于数列
行最后一项位于数列![]() 的项数为
的项数为![]() ,且
,且![]() ,
,
则![]() 位于数阵第
位于数阵第![]() 行第
行第![]() 项(即
项(即![]() ),
),
所以,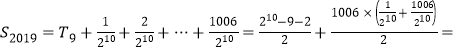
![]() ,命题③错误;
,命题③错误;
由①知,![]() ,且
,且![]() ,
,
则恰好满足![]() 的项
的项![]() 位于第
位于第![]() 行,假设位于第
行,假设位于第![]() 项,
项,
则有![]() ,可得出
,可得出![]() ,
,
由于![]() ,
,![]() ,则
,则![]() ,
,![]() ,
,
因此,满足![]() 的最小正整数
的最小正整数![]() ,命题④正确。
,命题④正确。
故选:B.


科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,椭圆
,椭圆![]() 与
与![]() 轴交于
轴交于![]() 两点,且
两点,且![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)设点![]() 是椭圆
是椭圆![]() 上的一个动点,且直线
上的一个动点,且直线![]() 与直线
与直线![]() 分别交于
分别交于![]() 两点.是否存在点
两点.是否存在点![]() 使得以
使得以![]() 为直径的圆经过点
为直径的圆经过点![]() ?若存在,求出点
?若存在,求出点![]() 的横坐标;若不存在,说明理由.
的横坐标;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设![]() 是椭圆
是椭圆![]()
![]() 的四个顶点,菱形
的四个顶点,菱形![]() 的面积与其内切圆面积分别为
的面积与其内切圆面积分别为![]() ,
, ![]() .椭圆
.椭圆![]() 的内接
的内接![]() 的重心(三条中线的交点)为坐标原点
的重心(三条中线的交点)为坐标原点![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2) ![]() 的面积是否为定值?若是,求出该定值,若不是,请说明理由.
的面积是否为定值?若是,求出该定值,若不是,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知f(x)是奇函数,且当x<0时,f(x)=x2+3x+2.若当x∈[1,3]时,n≤f(x)≤m恒成立,则m-n的最小值为( )
A. ![]() B. 2
B. 2
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从某校高三的学生中随机抽取了100名学生,统计了某次数学模考考试成绩如表:


(1)请在频率分布表中的①、②位置上填上相应的数据,并在给定的坐标系中作出这些数据的频率分布直方图,再根据频率分布直方图估计这100名学生的平均成绩;
(2)从这100名学生中,采用分层抽样的方法已抽取了 20名同学参加“希望杯数学竞赛”,现需要选取其中3名同学代表高三年级到外校交流,记这3名学生中“期中考试成绩低于120分”的人数为![]() ,求
,求![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(2016·威海模拟)三人参加某娱乐闯关节目,假设甲闯关成功的概率是![]() ,乙、丙两人同时闯关成功的概率是
,乙、丙两人同时闯关成功的概率是![]() ,甲、丙两人同时闯关失败的概率是
,甲、丙两人同时闯关失败的概率是![]() ,且三人各自能否闯关成功相互独立.
,且三人各自能否闯关成功相互独立.
(1)求乙、丙两人各自闯关成功的概率;
(2)设ξ表示三人中最终闯关成功的人数,求ξ的分布列和均值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com