练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    以下命题:①若|a·b|=|a|·|b|,则a∥b;②a=(-1,1)在b=(3,4)方向上的投影为;③若△ABC中,a="5,b=8," c=7,则·=20;④若非零向量a,b满足|a+b|=|b|,则|2b|>|a+2b|.其中所有真命题的序号是　　　　.
    ①②
    ①中,由|a·b|=|a||b||cos<a,b>|=|a||b|,知cos<a,b>=±1,故<a,b>=0或<a,b>=π,所以a∥b,故正确;②中a在b方向上的投影为|a|·cos<a,b>=|a|·=,故正确;③中,由余弦定理得cosC==,故·=-·=-5×8×=-20,故错误.④中,由|a+b|=|b|知|b|+|a+b|=|b|+|b|,∴|2b|=|b|+|a+b|≥|b+a+b|=|a+2b|,故错误.
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：不详 题型：单选题

    若向量两两所成的角相等，且，则等于（）
    A．B．C．或D．或

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：单选题

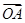    已知点A、B、C是直线l上不同的三个点，点O不在直线l上，则关于x的方程x2＋x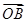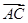＋＝0的解集为(  )
    A．∅B．{－1}
    C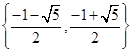．D．{－1,0}

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：填空题

    向量a，b，c满足：|a|＝1，|b|＝，b在a方向上的投影为，(a－c)·(b－c)＝0，则|c|的最大值是________．

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：单选题

    圆C:x2+y2=1,直线l:y=kx+2,直线l与圆C交于A,B,若|+|<|-|(其中O为坐标原点),则k的取值范围是(　　)
    A．(0,)B．(-,)
    C．(,+∞)D．(-∞,-)∪(,+∞)

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：单选题

    如图,在直角梯形ABCD中,AB∥CD,AD=CD=1,AB=3,动点P在△BCD内运动(含边界),设=α+β,则α+β的最大值是(　　)
    A．B．C．D．

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：单选题

    设A1,A2,A3,A4,A5是平面上给定的5个不同点,则使++++=0成立的点M的个数为(　　)
    A．0B．1C．5D．10

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：解答题

    已知a＝(sin α，1), b＝(cos α，2)，α∈.
    (1)若a∥b，求tan α的值；
    (2)若a·b＝，求sin 的值．

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：填空题

    如图，平行四边形中，是边上一点，为与的交点，且，若，，则用表示             .

    查看答案和解析>>

    同步练习册答案