解:(1)∵f(x)≤0的解集有且只有一个元素,
∴△=a
2-4a=0
∴a=0或4,
当a=0时,函数f(x)=x
2在(0,+∞)上递增,故不存在0<x
1<x
2,使得不等式f(x
1)>f(x
2)成立;
当a=4时,函数f(x)=x
2-4x+4在(0,2)上递减,故存在0<x
1<x
2,使得不等式f(x
1)>f(x
2)成立.
综上,得a=4,f(x)=x
2-4x+4,∴S
n=n
2-4n+4
n≥2 时,a
n=S
n-S
n-1=2n-5,n=1 时,a
1=1
∴a
n=

(2)∵c
n=1-
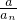
,
∴

∵n≥3时,C
n+1-C
n=
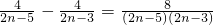
>0,
∴n≥3时,数列{c
n}递增,
∵a
4=-

<0,由
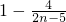
>0
n≥5,可知a
4-a
5<0,即n≥3时,有且只有1个变号数;
又∵C
1=-3,C
2=-5,C
3=-3,即C
1-C
2<0,C
2-C
3<0,
∴此处变号数有2个.
综上得数列共有3个变号数,即变号数为3.
分析:(1)根据f(x)≤0的解集有且只有一个元素,可得△等于0,从而可求a的值,即可求出函数解析式,从而可求数列{a
n}的通项公式;
(2))根据c
n=1-
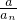
,可得

,验证n≥3时,数列{c
n}递增,确定n≥3时,有且只有1个变号数;判断n≤2时变号数有2个,最后综合答案可得.
点评:本题考查数列与函数的综合,考查数列的通项,考查新定义,解题的关键是理解新定义,判断数列的单调性,从而确定数列的变号数.

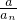 (n为正整数),求数列{cn}的变号数.
(n为正整数),求数列{cn}的变号数.
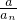 ,
,
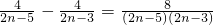 >0,
>0, <0,由
<0,由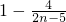 >0
>0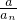 ,可得
,可得 ,验证n≥3时,数列{cn}递增,确定n≥3时,有且只有1个变号数;判断n≤2时变号数有2个,最后综合答案可得.
,验证n≥3时,数列{cn}递增,确定n≥3时,有且只有1个变号数;判断n≤2时变号数有2个,最后综合答案可得.

 名校课堂系列答案
名校课堂系列答案 已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<
已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<