练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】某研究型学习小组调查研究高中生使用智能手机对学习的影响，部分统计数据如下：

    使用智能手机

    不使用智能手机

    合计

    学习成绩优秀

    学习成绩不优秀

    合计

    （1）根据以上统计数据，你是否有 的把握认为使用智能手机对学习有影响？

    （2）为了进一步了解学生对智能手机的使用习惯，现在对以上使用智能手机的高中时采用分层抽样的方式，抽取一个容量为 的样本，若抽到的学生中成绩不优秀的比成绩优秀的多 人，求 的值.

    【答案】（1）有；（2）.

    【解析】分析：(1) 根据所给的数据做出这组数据的观测值，把观测值同临界值进行比较，得到该研究小组有99.5%的把握认为中学生使用智能手机对学习有影响；(2)根据分层抽样原则易得 的值.

    详解：（1），所以有99.5%的把握认为二者有关；

    （2）.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】如图，三棱柱ABC﹣A1B1C1中，AC=AA1=2，AB=BC=2 ，∠AA1C1=60°，平面ABC1⊥平面AA1C1C，AC1与A1C相交于点D．

    （1）求证：BC1⊥平面AA1C1C；
    （2）求二面角C1﹣AB﹣C的余弦值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在平面直角坐标系xOy中，以原点O为极点，x轴的非负半轴为极轴，建立极坐标系，若直线l的参数方程为 （t为参数，α为l的倾斜角），曲线E的极坐标方程为ρ=4sinθ．射线θ=β，θ=β+ ，θ=β﹣ 与曲线E分别交于不同于极点的三点A、B、C．
    （1）求证：|OB|+|OC|= |OA|；
    （2）当β= 时，直线l过B、C两点，求y0与α的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设集合A＝{x∈R|x2＋4x＝0}，B＝{x∈R|x2＋2(a＋1)x＋a2－1＝0，a∈R}，若BA，求实数a的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图所示，等腰梯形ABCD的底角A等于60°．直角梯形ADEF所在的平面垂直于平面 ABCD，∠EDA=90°，且ED=AD=2AF=2AB=2．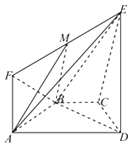

    （Ⅰ）证明：平面ABE⊥平面EBD；
    （Ⅱ）点M在线段EF上，试确定点M的位置，使平面MAB与平面ECD所成的角的余弦值为 ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数f（x）=ax（lnx﹣1）﹣x2（a∈R）恰有两个极值点x1 ， x2 ， 且x1＜x2 ． （Ⅰ）求实数a的取值范围；
    （Ⅱ）若不等式lnx1+λlnx2＞1+λ恒成立，求实数λ的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】对于下列说法正确的是（ ）
    A.若f（x）是奇函数，则f（x）是单调函数
    B.命题“若x2﹣x﹣2=0，则x=1”的逆否命题是“若x≠1，则x2﹣x﹣2=0”
    C.命题p：?x∈R，2x＞1024，则￢p：?x0∈R，
    D.命题“?x∈（﹣∞，0），2x＜x2”是真命题

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】记Sn为等比数列的前n项和，已知S2=2，S3=-6.

    （1）求的通项公式；

    （2）求Sn，并判断Sn+1，Sn，Sn+2是否成等差数列。

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】（本小题满分分）

    已知圆，过点作直线交圆于、两点．

    （Ⅰ）当经过圆心时，求直线的方程．

    （Ⅱ）当直线的倾斜角为时，求弦的长．

    （Ⅲ）求直线被圆截得的弦长时，求以线段为直径的圆的方程．

    查看答案和解析>>

    同步练习册答案