
【题目】某池塘中原有一块浮草,浮草蔓延后的面积y(m2)与时间t(月)之间的函数关系是y=at﹣1(a>0,且a≠1),它的图象如图所示.给出以下命题: ①池塘中原有浮草的面积是0.5m2;
②到第7个月浮草的面积一定能超过60m2
③浮草每月增加的面积都相等;
④若浮草面积达到4m2 , 16m2 , 64m2所经过时间分别为t1 , t2 , t3 , 则t1+t2<t3 , 其中所有正确命题的序号是( )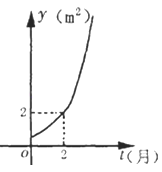
A.①②
B.①④
C.②③
D.②④
【答案】A
【解析】解答:根据图象过点(2,2)可知点(2,2)适合y=at﹣1即2=a
∴函数关系是y=2t﹣1
令t=0时,y= ![]() =0.5,故①正确;
=0.5,故①正确;
令t=7时,y=26=64>60,故②正确;
当t=1时,y=1,增加0.5,当t=2时,y=2,增加1,每月增加的面积不相等,故③不正确;
分别令y=4、16、64,解得t1=3,t2=5,t3=7,t1+t2>t3 , 故④不正确.
其中所有正确命题的序号是:①②
故选A.
分析:先根据图象经过点(2,2)求出a,代入函数的解析式,即可求出底数a,进而即可求出这个指数函数的表达式;然后对各个选择支进行逐一判断即可.令t=0时,y= ![]() =0.5即可对①进行判断;对于②,将t=7代入函数的解析式,即可求出第7个月时浮萍的面积;对于③,当t=1时,和当t=2时,计算这两个月增加的面积;分别将y=4、16、64分别代入函数解析式,求出对应的t值,即可对于④进行判断.
=0.5即可对①进行判断;对于②,将t=7代入函数的解析式,即可求出第7个月时浮萍的面积;对于③,当t=1时,和当t=2时,计算这两个月增加的面积;分别将y=4、16、64分别代入函数解析式,求出对应的t值,即可对于④进行判断.


 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案科目:高中数学 来源: 题型:
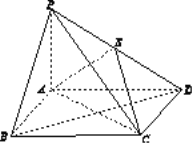
【题目】(本题满分12分)如图13,四棱锥P ABCD中,底面ABCD为矩形,PA⊥平面ABCD,E为PD的中点.
(1)证明:PB∥平面AEC;
(2)设AP=1,AD=![]() ,三棱锥P ABD的体积V=
,三棱锥P ABD的体积V=![]() ,求A到平面PBC的距离.
,求A到平面PBC的距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知在四棱锥S﹣ABCD中,底面ABCD是菱形,且∠BCD=60°,侧面SAB是正三角形,且面SAB⊥面ABCD,F为SD的中点. 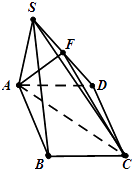
(1)证明:SB∥面ACF;
(2)求面SBC与面SAD所成锐二面角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)对任意的x,y∈R,总有f(x)+f(y)=f(x+y),且x<0时,f(x)>0.
(1)求证:函f(x)是奇函数;
(2)求证:函数f(x)是R上的减函数;
(3)若定义在(﹣2,2)上的函数f(x)满足f(﹣m)+f(1﹣m)<0,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给出三种函数模型:f(x)=xn(n>0),g(x)=ax(a>1)和h(x)=logax(a>1).根据它们增长的快慢,则一定存在正实数x0 , 当x>x0时,就有( )
A.f(x)>g(x)>h(x)
B.h(x)>g(x)>f(x)
C.f(x)>h(x)>g(x)
D.g(x)>f(x)>h(x)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)的定义域为(﹣2,2),函数g(x)=f(x﹣1)+f(3﹣2x).
(1)求函数g(x)的定义域;
(2)若f(x)是奇函数且在定义域内单调递减,求不等式g(x)≤0的解集
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com