
【题目】设f(x)是定义域为R的周期函数,最小正周期为2,且
f(1+x)=f(1-x),当-1≤x≤0时,f(x)=-x.
(1)判断f(x)的奇偶性;
(2)试求出函数f(x)在区间[-1,2]上的表达式.
【答案】(1) f(x)是偶函数(2) 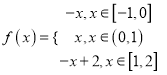
【解析】试题分析:(1)因为f(1+x)=f(1-x),所以f(-x)=f(2+x),又f(x)是最小正周期为 2的函数,所以f(x+2)=f(x),则 f(-x)=f(x),所以得f(x)是偶函数;
(2)由-1≤x≤0时,f(x)=-x,根据f(x)是偶函数得当0≤x≤1时,f(x)解析式;由f(x)是最小正周期为 2的函数,得1≤x≤2时,f(x)解析式.
试题解析:
(1)∵f(1+x)=f(1-x),∴f(-x)=f(2+x).
又f(x+2)=f(x),∴f(-x)=f(x).
又f(x)的定义域为R,
∴f(x)是偶函数.
(2)当x∈[0,1]时,-x∈[-1,0],
则f(x)=f(-x)=x;
进而当1≤x≤2时,-1≤x-2≤0,
f(x)=f(x-2)=-(x-2)=-x+2.
故


科目:高中数学 来源: 题型:
【题目】据某气象中心观察和预测:发生于M地的沙尘暴一直向正南方向移动,其移动速度v(km/h)与时间t(h)的函数图象如图所示.过线段OC上一点T(t,0)作横轴的垂线l,梯形OABC在直线l左侧部分的面积即时间t(h)内沙尘暴所经过的路程s(km).

(1)当t=4时,求s的值;
(2)将s随t变化的规律用数学关系式表示出来;
(3)若N城位于M地正南方向,且距M地650 km,试判断这场沙尘暴是否会侵袭到N城,如果会,在沙尘暴发生后多长时间它将侵袭到N城?如果不会,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】平面α外有两条直线m和n,如果m和n在平面α内的投影分别是m1和n1,给出下列四个命题:①m1⊥n1m⊥n;②m⊥nm1⊥n1;③m1与n1相交m与n相交或重合;④m1与n1平行m与n平行或重合.其中不正确的命题个数是( )
A. 1 B. 2
C. 3 D. 4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,其中
,其中![]() 为自然对数的底数.
为自然对数的底数.
(1)若函数![]() 在区间
在区间![]() 上是单调函数,试求实数
上是单调函数,试求实数![]() 的取值范围;
的取值范围;
(2)已知函数![]() ,且
,且![]() ,若函数
,若函数![]() 在区间
在区间![]() 上恰有3个零点,求实数
上恰有3个零点,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校为了鼓励学生热心公益,服务社会,成立了“慈善义工社”.2017年12月,该校“慈善义工社”为学生提供了4次参加公益活动的机会,学生可通过网路平台报名参加活动.为了解学生实际参加这4次活动的情况,该校随机抽取100名学生进行调查,数据统计如下表,其中“√”表示参加,“×”表示未参加.

(Ⅰ)从该校所有学生中任取一人,试估计其2017年12月恰参加了2次学校组织的公益活动的概率;
(Ⅱ)若在已抽取的100名学生中,2017年12月恰参加了1次活动的学生比4次活动均未参加的学生多17人,求![]() 的值;
的值;
(Ⅲ)若学生参加每次公益活动可获得10个公益积分,试估计该校4000名学生中,2017年12月获得的公益积分不少于30分的人数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,AC是圆O的直径,点B在圆O上,∠BAC=30°,BM⊥AC于点M,EA⊥平面ABC,FC∥EA,AC=4,EA=3,FC=1.

(1)证明:EM⊥BF;
(2)求平面BEF与平面ABC所成的锐二面角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数![]() ,
, ![]() (
(![]() ).
).
(1)当![]() 时,若函数
时,若函数![]() 与
与![]() 的图象在
的图象在![]() 处有相同的切线,求
处有相同的切线,求![]() 的值;
的值;
(2)当![]() 时,若对任意
时,若对任意![]() 和任意
和任意![]() ,总存在不相等的正实数
,总存在不相等的正实数![]() ,使得
,使得![]() ,求
,求![]() 的最小值;
的最小值;
(3)当![]() 时,设函数
时,设函数![]() 与
与![]() 的图象交于
的图象交于![]()
![]() 两点.求证:
两点.求证: ![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com