
分析 由题意和奇函数的定义f(-x)=-f(x)求出a的值,再由对数的真数大于零求出函数的定义域,则所给的区间应是定义域的子集,求出b的范围进而求出ab的范围.
解答 解:∵定义在区间(-b,b)内的函数f(x)=lg$\frac{1+2x}{1-ax}$是奇函数,
∴x∈(-b,b),f(-x)=-f(x),即lg$\frac{1-2x}{1+ax}$=-lg$\frac{1+2x}{1-ax}$,
∴1-a2x2=1-4x2,解得a=±2,
又∵a≠-2,∴a=2;则函数f(x)=lg$\frac{1+2x}{1-2x}$,
要使函数有意义,则$\frac{1+2x}{1-2x}$>0,即(1+2x)(1-2x)>0
解得:-$\frac{1}{2}$<x<$\frac{1}{2}$,即函数f(x)的定义域为:(-$\frac{1}{2}$,$\frac{1}{2}$),
∴(-b,b)⊆(-$\frac{1}{2}$,$\frac{1}{2}$),∴0<b≤$\frac{1}{2}$
∴ab的取值范围是(1,$\sqrt{2}$].
故答案为:(1,$\sqrt{2}$].
点评 本题考查了奇函数的定义以及求对数函数的定义域,利用子集关系求出b的范围,考查了学生的运算能力和对定义的运用能力.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
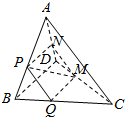 如图,在四面体ABCD中,截面PQMN是正方形,且PQ∥AC,则下列命题中,错误的是( )
如图,在四面体ABCD中,截面PQMN是正方形,且PQ∥AC,则下列命题中,错误的是( )| A. | AC⊥BD | B. | AC∥截面PQMN | ||
| C. | AC=BD | D. | 异面直线PM与BD所成的角为45° |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 若a∥b,a∥α,则b∥α | B. | 若a⊥b,a∥α,则b⊥α | C. | 若a∥b,a⊥α,则b⊥α | D. | 若a⊥b,a⊥α,则b∥α |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com