
【题目】如图,在四棱锥A﹣BCDE中,平面ABC⊥平面BCDE,∠CDE=∠BED=90°,AB=CD=2,DE=BE=1,AC= ![]() .
.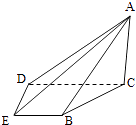
(Ⅰ)证明:AC⊥平面BCDE;
(Ⅱ)求直线AE与平面ABC所成的角的正切值.
【答案】解:(Ⅰ)如图所示,取DC的中点F,连接BF,则DF= ![]() DC=1=BE,
DC=1=BE,
∵∠CDE=∠BED=90°,∴BE∥DF,
∴四边形BEDF是矩形,
∴BF⊥DC,BF=ED=1,
在Rt△BCF中,BC= ![]() =
= ![]() .
.
在△ACB中,∵AB=2,BC=AC= ![]() ,
,
∴BC2+AC2=AB2,
∴AC⊥BC,
又平面ABC⊥平面BCDE,∴AC⊥平面BCDE.
(Ⅱ)过点E作EM⊥CB交CB的延长线于点M,连接AM.
又平面ABC⊥平面BCDE,∴EM⊥平面ACB.
∴∠EAM是直线AE与平面ABC所成的角.
在Rt△BEM中,EB=1,∠EBM=45°.
∴EM= ![]() =MB.
=MB.
在Rt△ACM中, ![]() =
= ![]() =
= ![]() .
.
在Rt△AEM中, ![]() =
= ![]() =
= ![]() .
.

【解析】91)根据勾股定理的逆定理可知AC⊥BC,由已知平面ABC⊥平面BCDE并且两平面相交于BC,根据直线和平面垂直的判定定理可知AC⊥平面BCDE。(2)根据题意作出辅助线,可证明EM⊥平面ACB进而可得∠EAM是直线AE与平面ABC所成的角,根据几何关系可求出tan的值。
【考点精析】本题主要考查了直线与平面垂直的判定和空间角的异面直线所成的角的相关知识点,需要掌握一条直线与一个平面内的两条相交直线都垂直,则该直线与此平面垂直;注意点:a)定理中的“两条相交直线”这一条件不可忽视;b)定理体现了“直线与平面垂直”与“直线与直线垂直”互相转化的数学思想;已知![]() 为两异面直线,A,C与B,D分别是
为两异面直线,A,C与B,D分别是![]() 上的任意两点,
上的任意两点,![]() 所成的角为
所成的角为![]() ,则
,则 才能正确解答此题.
才能正确解答此题.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】已知函数![]() ,若
,若![]()
(1)求![]() 的值,并写出函数
的值,并写出函数![]() 的最小正周期(不需证明);
的最小正周期(不需证明);
(2)是否存在正整数![]() ,使得函数
,使得函数![]() 在区间
在区间![]() 内恰有
内恰有![]() 个零点?若存在,求出
个零点?若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某企业生产A,B两种产品,根据市场调查与预测,A产品的利润与投资成正比,其关系如图①;B产品的利润与投资的算术平方根成正比,其关系如图②.(注:利润和投资单位:万元)
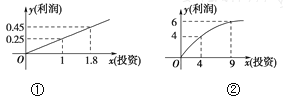
(1)分别将A,B两种产品的利润表示为投资的函数关系式;
(2)已知该企业已筹集到18万元资金,并将全部投入A,B两种产品的生产,怎样分配这18万元投资,才能使该企业获得最大利润?其最大利润约为多少万元?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱锥![]() 的底面
的底面![]() 是菱形,
是菱形,![]() ,
,![]() 平面
平面![]() ,
,![]() 是
是![]() 的中点.
的中点.
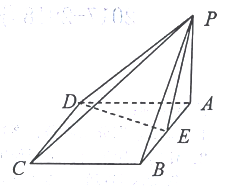
(1)求证:平面![]() 平面
平面![]() ;
;
(2)棱![]() 上是否存在一点
上是否存在一点![]() ,使得
,使得![]() 平面
平面![]() ?若存在,确定
?若存在,确定![]() 的位置并加以证明;若不存在,请说明理由.
的位置并加以证明;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知a,b,c分别为△ABC三个内角A,B,C的对边,ccosA+ ![]() csinA﹣b﹣a=0.
csinA﹣b﹣a=0.
(Ⅰ)求C;
(Ⅱ)若c=1,求△ABC的面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】利民中学为了了解该校高一年级学生的数学成绩,从高一年级期中考试成绩中抽出100名学生的成绩,由成绩得到如下的频率分布直方图.
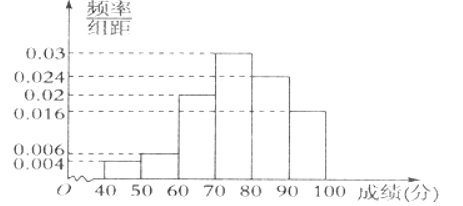
根据以上频率分布直方图,回答下列问题:
(1)求这100名学生成绩的及格率;(大于等于60分为及格)
(2)试比较这100名学生的平均成绩和中位数的大小.(精确到0.1)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com