
【题目】选修4—5:不等式选讲
设![]() .
.
(1)当![]() 时,解不等式
时,解不等式![]() ;
;
(2)若![]() 对任意
对任意![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
 走进文言文系列答案
走进文言文系列答案科目:高中数学 来源: 题型:
【题目】十九大提出:坚决打赢脱贫攻坚战,做到精准扶贫,某帮扶单位为帮助定点扶贫村真正脱贫,坚持扶贫同扶智相结合,帮助贫困村种植脐橙,并利用互联网电商进行销售,为了提高销量,现从该村的脐橙树上随机摘下100个脐橙进行测重,其质量(单位克)分布在区间[200,500内,由统计的质量数据作出频率分布直方图如图所示.

(1)按分层抽样的方法从质量在![]() ,
,![]() 的脐橙中随机抽取5个,再从这5个脐橙中随机抽取2个,求这2个脐橙质量至少有一个不小于400克的概率;
的脐橙中随机抽取5个,再从这5个脐橙中随机抽取2个,求这2个脐橙质量至少有一个不小于400克的概率;
(2)以各组数据的中间数值代替这组数据的平均值,以频率代替概率,已知该村的脐橙种植地上大约还有100000个脐橙待出售,某电商提出两种收购方案:
A.所有脐橙均以7元/千克收购;
B.低于350克的脐橙以2元/个收购,其余的以3元/个收购.
请你通过计算为该村选择收益较好的方案.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校组织由5名学生参加的演讲比赛,采用抽签法决定演讲顺序,在“学生![]() 和
和![]() 都不是第一个出场,
都不是第一个出场,![]() 不是最后一个出场”的前提下,学生
不是最后一个出场”的前提下,学生![]() 第一个出场的概率为( )
第一个出场的概率为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某厂销售部以箱为单位销售某种零件,每箱的定价为![]() 元,低于
元,低于![]() 箱按原价销售,不低于
箱按原价销售,不低于![]() 箱则有以下两种优惠方案:①以
箱则有以下两种优惠方案:①以![]() 箱为基准,每多
箱为基准,每多![]() 箱送
箱送![]() 箱;②通过双方议价,买方能以优惠
箱;②通过双方议价,买方能以优惠![]() 成交的概率为
成交的概率为![]() ,以优惠
,以优惠![]() 成交的概率为
成交的概率为![]() .
.
![]() 甲、乙两单位都要在该厂购买
甲、乙两单位都要在该厂购买![]() 箱这种零件,两单位都选择方案②,且各自达成的成交价格相互独立,求甲单位优惠比例不低于乙单位优惠比例的概率;
箱这种零件,两单位都选择方案②,且各自达成的成交价格相互独立,求甲单位优惠比例不低于乙单位优惠比例的概率;
![]() 某单位需要这种零件
某单位需要这种零件![]() 箱,以购买总价的数学期望为决策依据,试问该单位选择哪种优惠方案更划算?
箱,以购买总价的数学期望为决策依据,试问该单位选择哪种优惠方案更划算?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】由于浓酸泄漏对河流形成了污染,现决定向河中投入固体碱,1个单位的固体碱在水中逐步溶化,水中的碱浓度![]() 与时间
与时间![]() 的关系,可近似地表示为
的关系,可近似地表示为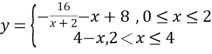 ,只有当河流中碱的浓度不低于1时,才能对污染产生有效的抑制作用.
,只有当河流中碱的浓度不低于1时,才能对污染产生有效的抑制作用.
(1)如果只投放1个单位的固体碱,则能够维持有效抑制作用的时间有多长?
(2)当河中的碱浓度开始下降时,即刻第二次投放1个单位的固体碱,此后,每一时刻河中的碱浓度认为是各次投放的碱在该时刻相应的碱浓度的和,求河中碱浓度可能取得的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com