
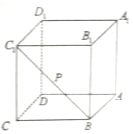
 如图,点P是正方体ABCD-A1B1C1D1的面对角线BC1(线段BC1)上运动,给出下列五个命题:
如图,点P是正方体ABCD-A1B1C1D1的面对角线BC1(线段BC1)上运动,给出下列五个命题:分析 对于①,根据异面直线的判定定理,可得结论;
对于②,连接A1B,A1C1容易证明平面BA1C1∥面ACD1,从而由线面平行的定义可得;
对于③,容易证明AD1∥BC1,从而BC1∥平面AD1C,以P为顶点,平面AD1C为底面,易得;
对于④,容易证明PDB1⊥面ACD1,从而可以证明面面垂直;
对于⑤,可以从向量的角度进行判断;
解答 解:对于①:AD∥平面B1C1CB,B1P?平面B1C1CB,B1P与AD不平行,故直线AD与直线B1P为异面直线;①正确;
对于②:连接A1B,A1C1,可得平面BA1C1∥面ACD1,∵A1P?平面BA1C1,故A1P∥平面ACD1;②正确;
对于③:容易证明AD1∥BC1,从而BC1∥平面AD1C,故BC1上任意一点到平面AD1C的距离均相等,所以以P为顶点,平面AD1C为底面,则三棱锥A-D1PC的体积不变;③正确;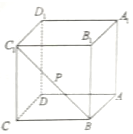
对于④:连接DB1,由DB1⊥AC且DB1⊥AD1,
可得DB1⊥面ACD1,从而由面面垂直的判定知,故④正确;
对于⑤:∵随着P点的移动,$\overrightarrow{AP}$与平面ACD1的法向量的夹角也是变化的,∴⑤错误
故答案为:①②③④
点评 本题考查三棱锥体积求法中的等体积法;线面平行、垂直的判定,要注意使用转化的思想.


科目:高中数学 来源: 题型:解答题
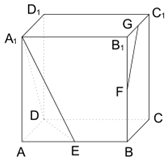 如 图,正方体ABCD-A1B1C1D1的棱长为2,E、F、G 分别为 AB、BB1、B1C1 的中点.
如 图,正方体ABCD-A1B1C1D1的棱长为2,E、F、G 分别为 AB、BB1、B1C1 的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
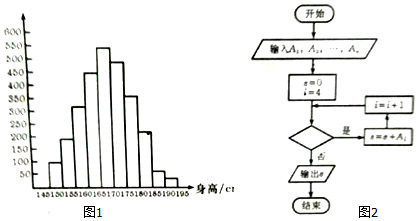
| A. | i<6 | B. | i<7 | C. | i<8 | D. | i<9 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [0,2] | B. | (0,2) | C. | (-∞,0)∪(2,+∞) | D. | (-∞,-2] |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-1)n-1$\frac{1}{{3}^{n}}$ | B. | (-1)n-1$\frac{1}{3n}$ | C. | (-1)n$\frac{1}{{3}^{n}}$ | D. | (-1)n$\frac{1}{3n}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{6}$ | B. | $\sqrt{3}$ | C. | $\frac{2\sqrt{3}}{3}$ | D. | $\frac{2\sqrt{6}}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
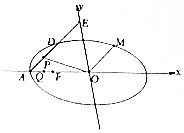 已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{12}$=1(a>2$\sqrt{3}$)的左焦点为F,左顶点为A,$\frac{1}{|OF|}$+$\frac{1}{|OA|}$=$\frac{3e}{|FA|}$,其中O为原点,e为椭圆的离心率,过点A作斜率为k(k≠0)的直线l交椭圆C于点D,交y轴于点E.
已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{12}$=1(a>2$\sqrt{3}$)的左焦点为F,左顶点为A,$\frac{1}{|OF|}$+$\frac{1}{|OA|}$=$\frac{3e}{|FA|}$,其中O为原点,e为椭圆的离心率,过点A作斜率为k(k≠0)的直线l交椭圆C于点D,交y轴于点E.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com