
【题目】已知数列![]() 的前
的前![]() 项和为
项和为![]() ,
, ![]() .
.
(1)求数列![]() 的通项公式;
的通项公式;
(2)令![]() ,设数列
,设数列![]() 的前
的前![]() 项和为
项和为![]() ,求
,求![]() ;
;
(3)令![]() ,若
,若![]() 对
对![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
【答案】(1) ![]() ; (2)
; (2) ![]() ;(3)
;(3) ![]()
【解析】试题分析:(1) 当![]() 时,利用公式
时,利用公式![]() ;,可得
;,可得![]() ,验证当
,验证当![]() 时是否适合即可;(2)由(1)可得
时是否适合即可;(2)由(1)可得![]() ,利用错位相减法求和即可(3)讨论当
,利用错位相减法求和即可(3)讨论当![]() 为奇数时,当
为奇数时,当![]() 为偶数时两种情况,分别利用等差数列求和公式求和,然后利用放缩法可证明结论.
为偶数时两种情况,分别利用等差数列求和公式求和,然后利用放缩法可证明结论.
试题解析:(I)当![]() 时,
时, ![]()
当![]() 时,
时, ![]() ,适合上式,
,适合上式,
![]()
![]() (
(![]() ).
).
(II) ![]() ,则
,则![]() ,
,
![]() ,
,
-得
![]() ,
,
![]() .
.
![]() .
.
(III) ![]() ,
,
当![]() 为奇数时,
为奇数时, ![]() ,
, ![]()
![]()
![]()
![]()
![]()
![]()
当![]() 为偶数时,
为偶数时, ![]() ,
,
![]()
![]()
![]()
![]()
![]()
![]()
综上所述, ![]()
【 方法点睛】本题主要考查等差数列的通项与求和公式以及错位相减法求数列的的前![]() 项和,属于中档题.一般地,如果数列
项和,属于中档题.一般地,如果数列![]() 是等差数列,
是等差数列, ![]() 是等比数列,求数列
是等比数列,求数列![]() 的前
的前![]() 项和时,可采用“错位相减法”求和,一般是和式两边同乘以等比数列
项和时,可采用“错位相减法”求和,一般是和式两边同乘以等比数列![]() 的公比,然后作差求解, 在写出“
的公比,然后作差求解, 在写出“![]() ”与“
”与“![]() ” 的表达式时应特别注意将两式“错项对齐”以便下一步准确写出“
” 的表达式时应特别注意将两式“错项对齐”以便下一步准确写出“![]() ”的表达式.
”的表达式.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】某中学将100名高二文科生分成水平相同的甲、乙两个“平行班”,每班50人.陈老师采用A,B两种不同的教学方式分别在甲、乙两个班进行教改实验.为了了解教学效果,期末考试后,陈老师对甲、乙两个班级的学生成绩进行统计分析,画出频率分布直方图(如下图).记成绩不低于90分者为“成绩优秀”.

(Ⅰ)根据频率分布直方图填写下面2×2列联表;
甲班(A方式) | 乙班(B方式) | 总计 | |
成绩优秀 | |||
成绩不优秀 | |||
总计 |
(Ⅱ)判断能否在犯错误的概率不超过0.05的前提下认为:“成绩优秀”与教学方式有关?
附:![]() .
.
P(K2≥k) | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 |
k | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】有下列四个命题:
①“若![]() , 则
, 则![]() 互为相反数”的逆命题;
互为相反数”的逆命题;
②“若两个三角形全等,则两个三角形的面积相等”的否命题;
③“若![]() ,则
,则![]() 有实根”的逆否命题;
有实根”的逆否命题;
④“若![]() 不是等边三角形,则
不是等边三角形,则![]() 的三个内角相等”逆命题;
的三个内角相等”逆命题;
其中真命题为( ).
A. ①② B. ②③ C. ①③ D. ③④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知过原点的动直线![]() 与圆
与圆![]() 相交于不同的两点
相交于不同的两点![]() ,
, ![]() .
.
(1)求圆![]() 的圆心坐标;
的圆心坐标;
(2)求线段![]() 的中点
的中点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(3)是否存在实数![]() ,使得直线
,使得直线![]() 与曲线
与曲线![]() 只有一个交点?若存在,求出
只有一个交点?若存在,求出![]() 的取值范围;若不存在,说明理由.
的取值范围;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,在直四棱柱ABCD﹣A1B1C1D1中,DB=BC,DB⊥AC,点M是棱BB1上一点.
(1)求证:B1D1∥面A1BD;
(2)求证:MD⊥AC;
(3)试确定点M的位置,使得平面DMC1⊥平面CC1D1D.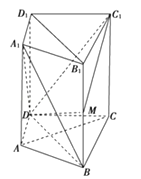
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com