
【题目】f(x)的定义域为(0,+∞),且对一切x>0,y>0都有f![]() =f(x)-f(y),当x>1时,有f(x)>0。
=f(x)-f(y),当x>1时,有f(x)>0。
(1)求f(1)的值;
(2)判断f(x)的单调性并证明;
(3)若f(6)=1,解不等式f(x+3)-f![]() <2;
<2;
(4)若f(4)=2,求f(x)在[1,16]上的值域。
【答案】(1)0,(2)见解析(3)![]() (4)
(4)![]()
【解析】
(1)利用赋值法令x=y,进行求解即可.
(2)利用抽象函数的关系,结合函数单调性的定义进行证明即可.
(3)利用函数单调性的性质将不等式进行转化求解即可.
(4)根据(2)的结论,将值域问题转化为求最值,根据f(4)=2,结合f(![]() )=f(x)﹣f(y),赋值x=16,y=4,代入即可求得f(16),从而求得f(x)在[1,16]上的值域
)=f(x)﹣f(y),赋值x=16,y=4,代入即可求得f(16),从而求得f(x)在[1,16]上的值域
(1)令x=y,f(1)=f(![]() )=f(x)﹣f(x)=0,x>0
)=f(x)﹣f(x)=0,x>0
(2)设0<x1<x2,则由f(![]() )=f(x)﹣f(y),得f(x2)﹣f(x1)=f(
)=f(x)﹣f(y),得f(x2)﹣f(x1)=f(![]() ),
),
∵![]() >1,∴f(
>1,∴f(![]() )>0.∴f(x2)﹣f(x1)>0,即f(x)在(0,+∞)上是增函数
)>0.∴f(x2)﹣f(x1)>0,即f(x)在(0,+∞)上是增函数
(3)∵f(6)=f(![]() )=f(36)﹣f(6),∴f(36)=2,
)=f(36)﹣f(6),∴f(36)=2,
原不等式化为f(x2+3x)<f(36),∵f(x)在(0,+∞)上是增函数,
∴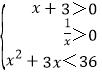 解得0<x<
解得0<x<![]() .故原不等式的解集为(0,
.故原不等式的解集为(0,![]() )
)
(4)由(2)知f(x)在[1,16]上是增函数.
∴f(x)min=f(1)=0,f(x)max=f(16).
∵f(4)=2,由f(![]() )=f(x)﹣f(y),知f(
)=f(x)﹣f(y),知f(![]() )=f(16)﹣f(4),
)=f(16)﹣f(4),
∴ f(16)=2f(4)=4,∴ f(x)在[1,16]上的值域为[0,4]


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】某竞赛的题库系统有60%的自然科学类题目,40%的文化生活类题目(假设题库中的题目总数非常大),参赛者需从题库中抽取3个题目作答,有两种抽取方法:方法一是直接从题库中随机抽取3个题目;方法二是先在题库中按照题目类型用分层抽样的方法抽取10个题目作为样本,再从这10个题目中任意抽取3个题目.
(1)两种方法抽取的3个题目中,恰好有1个自然科学类题目和2个文化生活类题目的概率是否相同?若相同,说明理由;若不同,分别计算出两种抽取方法对应的概率.
(2)已知某参赛者抽取的3个题目恰好有1个自然科学类题目和2个文化生活类题目,且该参赛者答对自然科学类题目的概率为![]() ,答对文化生活类题目的概率为
,答对文化生活类题目的概率为![]() .设该参赛者答对的题目数为X,求X的分布列和数学期望.
.设该参赛者答对的题目数为X,求X的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某产品的广告费用x与销售额y的统计数据如下表:
广告费用x(万元) | 4 | 2 | 3 | 5 |
销售额y(万元) | 49 | 26 | 39 | 54 |
(1)求根据上表可得线性回归方程![]() =
=![]() x+
x+![]() ;
;
(2) 模型预报广告费用为6万元时销售额为多少
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某玩具生产公司每天计划生产卫兵、骑兵、伞兵这三种玩具共![]() 个,生产一个卫兵需
个,生产一个卫兵需![]() 分钟,生产一个骑兵需
分钟,生产一个骑兵需![]() 分钟,生产一个伞兵需
分钟,生产一个伞兵需![]() 分钟,已知总生产时间不超过
分钟,已知总生产时间不超过![]() 小时,若生产一个卫兵可获利润
小时,若生产一个卫兵可获利润![]() 元,生产一个骑兵可获利润
元,生产一个骑兵可获利润![]() 元,生产一个伞兵可获利润
元,生产一个伞兵可获利润![]() 元.
元.
(1)用每天生产的卫兵个数![]() 与骑兵个数
与骑兵个数![]() 表示每天的利润
表示每天的利润![]() (元);
(元);
(2)怎么分配生产任务才能使每天的利润最大,最大利润是多少?

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=cos ![]() ,g(x)=exf(x),其中e为自然对数的底数.
,g(x)=exf(x),其中e为自然对数的底数.
(1)求曲线y=g(x)在点(0,g(0))处的切线方程;
(2)若对任意 ![]() 时,方程g(x)=xf(x)的解的个数,并说明理由.
时,方程g(x)=xf(x)的解的个数,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】关于函数f(x)=sin(x﹣![]() )sin(x+
)sin(x+![]() ),有下列命题:
),有下列命题:
①此函数可以化为f(x)=﹣![]() sin(2x+
sin(2x+![]() );
);
②函数f(x)的最小正周期是π,其图象的一个对称中心是(![]() , 0);
, 0);
③函数f(x)的最小值为﹣![]() , 其图象的一条对称轴是x=
, 其图象的一条对称轴是x=![]() ;
;
④函数f(x)的图象向右平移![]() 个单位后得到的函数是偶函数;
个单位后得到的函数是偶函数;
⑤函数f(x)在区间(﹣![]() , 0)上是减函数.
, 0)上是减函数.
其中所有正确的命题的序号个数是( )
A.2
B.3
C.4
D.5
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】将函数f(x)=cos(ωx+φ)(ω>0,|φ|< ![]() )的图象上的每一点的纵坐标不变,横坐标缩短为原来的一半,再将图象向右平移
)的图象上的每一点的纵坐标不变,横坐标缩短为原来的一半,再将图象向右平移 ![]() 个单位长度得到函数y=sinx的图象.
个单位长度得到函数y=sinx的图象.
(1)直接写出f(x)的表达式,并求出f(x)在[0,π]上的值域;
(2)求出f(x)在[0,π]上的单调区间.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知方程C:x2+y2﹣2x﹣4y+m=0,
(1)若方程C表示圆,求实数m的范围;
(2)在方程表示圆时,该圆与直线l:x+2y﹣4=0相交于M、N两点,且|MN|=![]() ,求m的值.
,求m的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com