Question

下列说法中，正确的有

 

 （把所有正确的序号都填上）．
①“?x∈R，使2^x＞3“的否定是“?x∈R，使2^x≤3”；
②函数y=sin（2x+

π

3

）sin（

π

6

-2x）的最小正周期是π；
③命题“函数f（x）在x=x₀处有极值，则f'（x₀）=0”的否命题是真命题；
④函数f（x）=2^x-x²的零点有2个；
⑤

∫

1 -1

1-x2

dx等于

π

2

．

Answer 1

考点：命题的真假判断与应用

专题：简易逻辑

分析：通过命题的否定判断①的正误；函数的周期判断②的正误；命题的否命题的真假判断③的正误；函数的零点的公式判断④的正误；定积分求出值判断⑤的正误．

解答： 解：对于①“?x∈R，使2^x＞3“的否定是“?x∈R，使2^x≤3”，满足特称命题的否定是全称命题的形式，所以①正确；
对于②，函数y=sin（2x+

π

3

）sin（

π

6

-2x）=

1

2

sin（4x+

2π

3

），函数的最小正周期

π

2

，所以②不正确；
对于③，命题“函数f（x）在x=x₀处有极值，则f'（x₀）=0”的否命题是：若f'（x₀）=0，则函数f（x）在x=x₀处有极值，显然不正确．利用y=x³，x=0时，导数为0，但是x=0不是函数的极值点，所以是真命题；
所以③不正确；
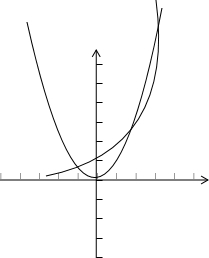
对于④，由题意可知：要研究函数f（x）=x²-2^x的零点个数，
只需研究函数y=2^x，y=x²的图象交点个数即可．画出函数y=2^x，y=x²的图象，由图象可得有3个交点．
所以④不正确；
对于⑤，

∫

1 -1

1-x2

dx的几何意义是半圆的面积，圆的面积为π，

∫

1 -1

1-x2

dx=

π

2

．所以⑤正确；
故答案为：①⑤．

点评：本题考查命题的真假的判断与应用，考查命题的否定，零点判定定理，定积分的求法，函数的周期等知识，考查基本知识的应用．