
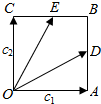
 如图所示,四边形OABC是边长为1的正方形,$\overrightarrow{OA}$=e1,$\overrightarrow{OC}$=e2,D、E分别为AB、BC中点.
如图所示,四边形OABC是边长为1的正方形,$\overrightarrow{OA}$=e1,$\overrightarrow{OC}$=e2,D、E分别为AB、BC中点.分析 ①运用向量的三角形法则,结合正方形的性质,即可得到所求向量;
②运用向量的数量积的性质,向量垂直的条件:数量积为0,向量的平方即为模的平方,计算即可得到所求;
③分别求得向量$\overrightarrow{OD}$,$\overrightarrow{OE}$的模,运用向量的夹角公式,计算整理即可得到所求值.
解答 解:①$\overrightarrow{OD}$=$\overrightarrow{OA}$+$\overrightarrow{AD}$=$\overrightarrow{OA}$+$\frac{1}{2}$$\overrightarrow{AB}$=$\overrightarrow{OA}$+$\frac{1}{2}$$\overrightarrow{OC}$=$\overrightarrow{{e}_{1}}$+$\frac{1}{2}$$\overrightarrow{{e}_{2}}$;
$\overrightarrow{OE}$=$\overrightarrow{OC}$+$\overrightarrow{CE}$=$\overrightarrow{OC}$+$\frac{1}{2}$$\overrightarrow{CB}$=$\overrightarrow{OC}$+$\frac{1}{2}$$\overrightarrow{OA}$=$\overrightarrow{{e}_{2}}$+$\frac{1}{2}$$\overrightarrow{{e}_{1}}$;
②$\overrightarrow{OD}$•$\overrightarrow{OE}$=($\overrightarrow{{e}_{1}}$+$\frac{1}{2}$$\overrightarrow{{e}_{2}}$)•($\overrightarrow{{e}_{2}}$+$\frac{1}{2}$$\overrightarrow{{e}_{1}}$)=$\frac{1}{2}$$\overrightarrow{{e}_{1}}$2+$\frac{1}{2}$$\overrightarrow{{e}_{2}}$2+$\frac{5}{4}$$\overrightarrow{{e}_{1}}$•$\overrightarrow{{e}_{2}}$
=$\frac{1}{2}$+$\frac{1}{2}$+0=1;
③|$\overrightarrow{OD}$|=$\sqrt{(\overrightarrow{{e}_{1}}+\frac{1}{2}\overrightarrow{{e}_{2}})^{2}}$=$\sqrt{{\overrightarrow{{e}_{1}}}^{2}+\frac{1}{4}{\overrightarrow{{e}_{2}}}^{2}+\overrightarrow{{e}_{1}}•\overrightarrow{{e}_{2}}}$=$\sqrt{1+\frac{1}{4}}$=$\frac{\sqrt{5}}{2}$,
|$\overrightarrow{OE}$|=$\sqrt{(\overrightarrow{{e}_{2}}+\frac{1}{2}\overrightarrow{{e}_{1}})^{2}}$=$\sqrt{{\overrightarrow{{e}_{2}}}^{2}+\frac{1}{4}{\overrightarrow{{e}_{1}}}^{2}+\overrightarrow{{e}_{1}}•\overrightarrow{{e}_{2}}}$=$\sqrt{1+\frac{1}{4}}$=$\frac{\sqrt{5}}{2}$,
即有cosθ=$\frac{\overrightarrow{OD}•\overrightarrow{OE}}{|\overrightarrow{OD}|•|\overrightarrow{OE}|}$=$\frac{1}{\frac{\sqrt{5}}{2}×\frac{\sqrt{5}}{2}}$=$\frac{4}{5}$.
点评 本题考查向量的数量积的坐标表示和向量夹角的求法,考查向量的加减运算,注意运用三角形法则,考查运算能力,属于中档题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com