
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
|
| 1 |
| 2 |
|
| 1 |
| 2 |
| 1 |
| 2 |
|
| 2a |
| 1+4a2 |
| 2a |
| 1+2a |
| 4a2 |
| 1+4a2 |
| 2a |
| 1+2a |
| 2a |
| 1+2a |
| 2a |
| 1+4a2 |
| 2a |
| 1+4a2 |
| 4a2 |
| 1+4a2 |
| 4a2 |
| 1+4a2 |
| 2a |
| 1+4a2 |
| 4a2 |
| 1+4a2 |
| 1 |
| 2 |
| 2a |
| 1+4a2 |
| 4a2 |
| 1+4a2 |
| 1 |
| 4a |
| 4a-1 |
| 4a |
| 1 |
| 4a |
| 2a-1 |
| 4(1+4a2) |
2(a-
| ||||||||
| (1+4a2)2 |
| 1 |
| 2 |
1+
| ||
| 2 |
1+
| ||
| 2 |
| 4a-1 |
| 4a |
| 8a2-6a+1 |
| 4(1+4a2) |
| 12a2+4a-3 |
| 2(1+4a2)2 |
| 1 |
| 2 |
| 12a2+4a-3 |
| 2(1+4a2)2 |
| 1 |
| 2 |


 șŁ”í»ÆžÔĂûÊŠ”ŒșœÏ”ÁĐŽđ°ž
șŁ”í»ÆžÔĂûÊŠ”ŒșœÏ”ÁĐŽđ°ž
| Äꌶ | žßÖĐżÎłÌ | Äꌶ | łőÖĐżÎłÌ |
| žßÒ» | žßÒ»Ăâ·ŃżÎłÌÍÆŒöŁĄ | łőÒ» | łőÒ»Ăâ·ŃżÎłÌÍÆŒöŁĄ |
| žß¶ț | žß¶țĂâ·ŃżÎłÌÍÆŒöŁĄ | łő¶ț | łő¶țĂâ·ŃżÎłÌÍÆŒöŁĄ |
| žßÈę | žßÈęĂâ·ŃżÎłÌÍÆŒöŁĄ | łőÈę | łőÈęĂâ·ŃżÎłÌÍÆŒöŁĄ |
żÆÄżŁșžßÖĐÊęѧ ÀŽÔŽŁș ÌâĐÍŁș
 Łš2013•œÎśŁ©ĐĄČšÒŃÓÎÏ··œÊœŸö¶šÊÇÈ„ŽòÇòĄąłȘžè»čÊÇÈ„ÏÂÆ棟ÓÎÏ·čæÔòÎȘÒÔOÎȘÆđ”㣏ÔÙŽÓA1ŁŹA2ŁŹA3ŁŹA4ŁŹA5ŁŹA6ŁšÈçÍŒŁ©Őâ6žö”ăÖĐÈÎÈĄÁœ”ă·Ö±đÎȘÖŐ”ă”Ă”œÁœžöÏòÁżŁŹŒÇŚĄŐâÁœžöÏòÁż”ÄÊęÁż»ęÎȘXŁŹÈôXŁŸ0ŸÍÈ„ŽòÇòŁŹÈôX=0ŸÍÈ„łȘžèŁŹÈôXŁŒ0ŸÍÈ„ÏÂÆć
Łš2013•œÎśŁ©ĐĄČšÒŃÓÎÏ··œÊœŸö¶šÊÇÈ„ŽòÇòĄąłȘžè»čÊÇÈ„ÏÂÆ棟ÓÎÏ·čæÔòÎȘÒÔOÎȘÆđ”㣏ÔÙŽÓA1ŁŹA2ŁŹA3ŁŹA4ŁŹA5ŁŹA6ŁšÈçÍŒŁ©Őâ6žö”ăÖĐÈÎÈĄÁœ”ă·Ö±đÎȘÖŐ”ă”Ă”œÁœžöÏòÁżŁŹŒÇŚĄŐâÁœžöÏòÁż”ÄÊęÁż»ęÎȘXŁŹÈôXŁŸ0ŸÍÈ„ŽòÇòŁŹÈôX=0ŸÍÈ„łȘžèŁŹÈôXŁŒ0ŸÍÈ„ÏÂÆćČ鿎Žđ°žșÍœâÎö>>
żÆÄżŁșžßÖĐÊęѧ ÀŽÔŽŁș ÌâĐÍŁș
Č鿎Žđ°žșÍœâÎö>>
żÆÄżŁșžßÖĐÊęѧ ÀŽÔŽŁș ÌâĐÍŁș
Č鿎Žđ°žșÍœâÎö>>
żÆÄżŁșžßÖĐÊęѧ ÀŽÔŽŁș ÌâĐÍŁș
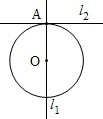 Łš2013•œÎśŁ©ÈçÍŒŁźÒŃÖȘl1ĄÍl2ŁŹÔČĐÄÔÚl1ÉÏĄą°ëŸ¶ÎȘ1m”ÄÔČOÔÚt=0ʱÓël2ÏàÇĐÓÚ”ăAŁŹÔČOŃŰl1ÒÔ1m/s”ÄËÙ¶ÈÔÈËÙÏòÉÏÒƶŻŁŹÔȱ»Ö±Ïßl2ËùœŰÉÏ·œÔČ»Ął€ŒÇÎȘxŁŹÁîy=cosxŁŹÔòyÓëʱŒätŁš0ĄÜtĄÜ1ŁŹ”„λŁșsŁ©”ÄșŻÊęy=fŁštŁ©”ÄÍŒÏóŽóÖÂÎȘŁšĄĄĄĄŁ©
Łš2013•œÎśŁ©ÈçÍŒŁźÒŃÖȘl1ĄÍl2ŁŹÔČĐÄÔÚl1ÉÏĄą°ëŸ¶ÎȘ1m”ÄÔČOÔÚt=0ʱÓël2ÏàÇĐÓÚ”ăAŁŹÔČOŃŰl1ÒÔ1m/s”ÄËÙ¶ÈÔÈËÙÏòÉÏÒƶŻŁŹÔȱ»Ö±Ïßl2ËùœŰÉÏ·œÔČ»Ął€ŒÇÎȘxŁŹÁîy=cosxŁŹÔòyÓëʱŒätŁš0ĄÜtĄÜ1ŁŹ”„λŁșsŁ©”ÄșŻÊęy=fŁštŁ©”ÄÍŒÏóŽóÖÂÎȘŁšĄĄĄĄŁ©Č鿎Žđ°žșÍœâÎö>>
°Ù¶ÈÖÂĐĆ - Á·Ï°ČáÁбí - ÊÔÌâÁбí
șț±±ÊĄ»„ÁȘÍű΄·šșÍČ»ÁŒĐĆÏąŸÙ±šÆœÌš | ÍűÉÏÓĐșŠĐĆÏąŸÙ±šŚšÇű | ”çĐĆŐ©ÆŸÙ±šŚšÇű | ÉæÀúÊ·ĐéÎȚÖśÒćÓĐșŠĐĆÏąŸÙ±šŚšÇű | ÉæÆóÇÖÈšŸÙ±šŚšÇű
΄·šșÍČ»ÁŒĐĆÏąŸÙ±š”ç»°Łș027-86699610 ŸÙ±šÓÊÏäŁș58377363@163.com