
【题目】已知数列![]() 满足
满足![]() ,
,![]() 时,
时,![]() .
.
(1)当![]() 时,求数列
时,求数列![]() 的前
的前![]() 项和
项和![]() ;
;
(2)当![]() 时,求证:对任意
时,求证:对任意![]() ,
,![]() 为定值.
为定值.
【答案】(1)![]() .(2)见解析
.(2)见解析
【解析】
(1)根据题意首先证明出该数列![]() 为等比数列,并把数值代入到等比数列的前
为等比数列,并把数值代入到等比数列的前![]() 项和公式计算出结果即可.
项和公式计算出结果即可.
(2)由已知可证出数列![]() 的通项公式,进而分析可得出这是一个等差等比结构,利用错位相减法求和可到
的通项公式,进而分析可得出这是一个等差等比结构,利用错位相减法求和可到![]() ,进而得到
,进而得到![]() 的通项公式,再对
的通项公式,再对![]() 分情况然后结合数学归纳法对上式进行推理证明即可.
分情况然后结合数学归纳法对上式进行推理证明即可.
解:(1)当![]() 时,
时,![]() .
.
数列![]() 是以
是以![]() ,公比为2的等比数列.
,公比为2的等比数列.
所以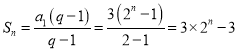 .
.
(2)当![]() 时,
时,![]() 时,
时,![]()
∴![]() .
.
令![]() ,∴
,∴![]()
∴![]() ①
①
 ,
,
这是一个等差乘等比结构,利用错位相减法求和
由![]() ②
②
两式①②相减得![]()
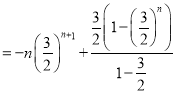
∴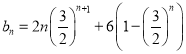
∴于是
∴![]() .
.
![]() ,
,![]() 为定值,
为定值,![]() 时,也满足,
时,也满足,
因此,对任意![]() ,
,![]() 为定值3.
为定值3.
(2)(数学归纳法)令![]() ,
,
当![]() 时,
时,![]() .
.
假设![]() 时命题成立,即
时命题成立,即![]() .
.
即![]()
由题设![]()
![]() .
.
所以![]() ,即
,即![]() 时,命题也成立
时,命题也成立
根据数学归纳原理,所命题得证.


 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案 小题狂做系列答案
小题狂做系列答案科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
已知平面直角坐标系![]() ,以
,以![]() 为极点,
为极点, ![]() 轴的非负半轴为极轴建立极坐标系,
轴的非负半轴为极轴建立极坐标系, ![]() 点的极坐标为
点的极坐标为![]() ,曲线
,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数).
为参数).
(1)写出点![]() 的直角坐标及曲线
的直角坐标及曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)若![]() 为曲线
为曲线![]() 上的动点,求
上的动点,求![]() 的中点
的中点![]() 到直线
到直线![]() :
: ![]() 的距离的最小值.
的距离的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的右焦点F到左顶点的距离为3.
的右焦点F到左顶点的距离为3.
(1)求椭圆C的方程;
(2)设O是坐标原点,过点F的直线与椭圆C交于A,B两点(A,B不在x轴上),若![]() ,延长AO交椭圆与点G,求四边形AGBE的面积S的最大值.
,延长AO交椭圆与点G,求四边形AGBE的面积S的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】自湖北武汉爆发新型冠状病毒肺炎疫情以来,各地医疗物资缺乏,各生产企业纷纷加班加点生产,某企业准备购买三台口罩生产设备,型号分别为A,B,C,已知这三台设备均使用同一种易耗品,提供设备的商家规定:可以在购买设备的同时购买该易耗品,每件易耗品的价格为100元;也可以在设备使用过程中,随时单独购买易耗品,每件易耗品的价格为200元.为了决策在购买设备时应同时购买的易耗品的件数,该单位调查了这三种型号的设备各60台,调查每台设备在一个月中使用的易耗品的件数,并得到统计表如下所示.
每台设备一个月中使用的易耗品的件数 | 6 | 7 | 8 | |
频数 | 型号A | 30 | 30 | 0 |
型号B | 20 | 30 | 10 | |
型号C | 0 | 45 | 15 | |
将调查的每种型号的设备的频率视为概率,各台设备在易耗品的使用上相互独立.
(1)求该单位一个月中A,B,C三台设备使用的易耗品总数超过21件(不包括21件)的概率;
(2)以该单位一个月购买易耗品所需总费用的期望值为决策依据,该单位在购买设备时应同时购买20件还是21件易耗品?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系xOy中,直线l的参数方程为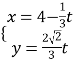 (其中t为参数).以坐标原点O为极点,x轴非负半轴为极轴建立极坐标系,曲线C的极坐标方程为
(其中t为参数).以坐标原点O为极点,x轴非负半轴为极轴建立极坐标系,曲线C的极坐标方程为![]() .
.
(1)求l和C的直角坐标方程.
(2)设点![]() ,直线l交曲线C于A,B两点,求
,直线l交曲线C于A,B两点,求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com