
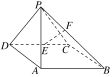
【题目】如图,在四棱锥PABCD中,侧面PAD⊥底面ABCD,底面ABCD是平行四边形,∠ABC=45°,AD=AP=2,AB=DP=![]() ,E为CD的中点,点F在线段PB上.试确定点F的位置,使得直线EF与平面PDC所成的角和直线EF与平面ABCD所成的角相等.
,E为CD的中点,点F在线段PB上.试确定点F的位置,使得直线EF与平面PDC所成的角和直线EF与平面ABCD所成的角相等.
【答案】当![]() 时,直线EF与平面PDC所成的角和直线EF与平面ABCD所成的角相等
时,直线EF与平面PDC所成的角和直线EF与平面ABCD所成的角相等
【解析】
由已知可证PA⊥底面ABCD,由余弦定理求出![]() ,进而有
,进而有![]() ,以A为坐标原点,以DA,AC,AP所在直线为x轴,y轴,z轴,建立空间直角坐标系Axyz,求出
,以A为坐标原点,以DA,AC,AP所在直线为x轴,y轴,z轴,建立空间直角坐标系Axyz,求出![]() 坐标,设
坐标,设![]() =λ(λ∈[0,1]),求出平面PDC的法向量坐标,而平面ABCD的一个法向量为
=λ(λ∈[0,1]),求出平面PDC的法向量坐标,而平面ABCD的一个法向量为![]() =(0,0,1),按照空间向量的线面角公式,即可求解.
=(0,0,1),按照空间向量的线面角公式,即可求解.
∵侧面PAD⊥底面ABCD,侧面PAD∩底面ABCD=AD,
PA⊥AD,PA平面PAD,∴PA⊥底面ABCD. 以A为坐标原点,
在![]() 中,
中,![]() ,
,
![]()
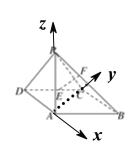
以DA,AC,AP所在直线为x轴,y轴,z轴,
建立如图所示的空间直角坐标系Axyz,
则A(0,0,0),D(-2,0,0),C(0,2,0),
B(2,2,0),E(-1,1,0),P(0,0,2),
∴![]() =(0,2,-2),
=(0,2,-2),![]() =(-2,0,-2),
=(-2,0,-2),
![]() =(2,2,-2).设
=(2,2,-2).设![]() =λ(λ∈[0,1]),
=λ(λ∈[0,1]),
则![]() =(2λ,2λ,-2λ),F(2λ,2λ,-2λ+2),
=(2λ,2λ,-2λ),F(2λ,2λ,-2λ+2),
∴![]() =(2λ+1,2λ-1,-2λ+2),
=(2λ+1,2λ-1,-2λ+2),
平面ABCD的一个法向量为![]() =(0,0,1).
=(0,0,1).
设平面PDC的法向量为![]() =(x,y,z),
=(x,y,z),
则∴![]() ,令x=1,得
,令x=1,得![]() =(1,-1,-1).
=(1,-1,-1).
∵直线EF与平面PDC所成的角和此直线与平面ABCD所成的角相等,
![]()
![]() ,
,
即![]() ,∴2-2λ=
,∴2-2λ=![]() ,解得
,解得![]() ,
,
∴当![]() 时,直线EF与平面PDC所成的角和直线EF与平面ABCD所成的角相等.
时,直线EF与平面PDC所成的角和直线EF与平面ABCD所成的角相等.


科目:高中数学 来源: 题型:
【题目】近年来,昆明加大了特色农业建设,其中花卉产业是重要组成部分.昆明斗南毗邻滇池东岸,是著名的花都,有“全国10支鲜花7支产自斗南”之说,享有“金斗南”的美誉.为进一步了解鲜花品种的销售情况,现随机抽取甲、乙两户斗南花农,对其连续5日的玫瑰花日销售情况进行跟踪调查,将日销售量作为样本绘制成茎叶图如下,单位:扎(20支/扎).
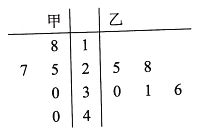
(1)求甲、乙两户花农连续5日的日均销售量,并比较两户花农连续5日销售量的稳定性;
(2)从两户花农连续5日的销售量中各随机抽取一个,求甲的销售量比乙的销售量高的概率·
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】足球是世界普及率最高的运动,我国大力发展校园足球.为了解本地区足球特色学校的发展状况,社会调查小组得到如下统计数据:
年份x | 2014 | 2015 | 2016 | 2017 | 2018 |
足球特色学校y(百个) | 0.30 | 0.60 | 1.00 | 1.40 | 1.70 |
(1)根据上表数据,计算y与x的相关系数r,并说明y与x的线性相关性强弱.
(已知:![]() ,则认为y与x线性相关性很强;
,则认为y与x线性相关性很强;![]() ,则认为y与x线性相关性一般;
,则认为y与x线性相关性一般;![]() ,则认为y与x线性相关性较):
,则认为y与x线性相关性较):
(2)求y关于x的线性回归方程,并预测A地区2020年足球特色学校的个数(精确到个).
参考公式和数据: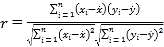 ,
,
![]()
![]()
![]() ,
,
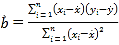
![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《九章算术》中《方田》章有弧田面积计算问题,计算术曰:以弦乘矢,矢又自乘,并之,二而一.其大意是,弧田面积计算公式为:弧田面积![]() (弦乘矢+矢乘矢),弧田是由圆弧(简称为弧田的弧)和以圆弧的端点为端点的线段(简称 (弧田的弦)围成的平面图形,公式中“弦”指的是弧田的弦长,“矢”等于弧田的弧所在圆的半径与圆心到弧田的弦的距离之差.现有一弧田,其弦长
(弦乘矢+矢乘矢),弧田是由圆弧(简称为弧田的弧)和以圆弧的端点为端点的线段(简称 (弧田的弦)围成的平面图形,公式中“弦”指的是弧田的弦长,“矢”等于弧田的弧所在圆的半径与圆心到弧田的弦的距离之差.现有一弧田,其弦长![]() 等于
等于![]() ,其弧所在圆为圆
,其弧所在圆为圆![]() ,若用上述弧田面积计算公式计算得该弧田的面积为
,若用上述弧田面积计算公式计算得该弧田的面积为![]() ,则
,则![]() ( )
( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在平行六面体ABCD-A1B1C1D1中,AA1⊥平面ABCD,且AB=AD=2,AA1=![]() ,∠BAD=120°.
,∠BAD=120°.
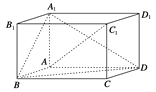
(1)求异面直线A1B与AC1所成角的余弦值;
(2)求二面角B-A1D-A的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
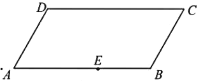
【题目】下图是一块平行四边形园地![]() ,经测量,
,经测量,![]()
![]() .拟过线段
.拟过线段![]() 上一点
上一点![]() 设计一条直路
设计一条直路![]() (点
(点![]() 在四边形
在四边形![]() 的边上,不计直路的宽度),将该园地分为面积之比为
的边上,不计直路的宽度),将该园地分为面积之比为![]() 的左,右两部分分别种植不同花卉.设
的左,右两部分分别种植不同花卉.设![]() (单位:m).
(单位:m).
(1)当点![]() 与点
与点![]() 重合时,试确定点
重合时,试确定点![]() 的位置;
的位置;
(2)求![]() 关于
关于![]() 的函数关系式;
的函数关系式;
(3)试确定点![]() 的位置,使直路
的位置,使直路![]() 的长度最短.
的长度最短.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为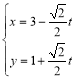 (
(![]() 为参数),在以坐标原点为极点,
为参数),在以坐标原点为极点,![]() 轴正半轴为极轴的极坐标系中,曲线
轴正半轴为极轴的极坐标系中,曲线![]() 的方程为
的方程为![]() .
.
(1)求曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)设曲线![]() 与直线
与直线![]() 交于点
交于点![]() ,点
,点![]() 的坐标为(3,1),求
的坐标为(3,1),求![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() 和圆
和圆![]() ,抛物线
,抛物线![]() 的焦点为
的焦点为![]() .
.

(1)求![]() 的圆心到
的圆心到![]() 的准线的距离;
的准线的距离;
(2)若点![]() 在抛物线
在抛物线![]() 上,且满足
上,且满足![]() , 过点
, 过点![]() 作圆
作圆![]() 的两条切线,记切点为
的两条切线,记切点为![]() ,求四边形
,求四边形![]() 的面积的取值范围;
的面积的取值范围;
(3)如图,若直线![]() 与抛物线
与抛物线![]() 和圆
和圆![]() 依次交于
依次交于![]() 四点,证明:
四点,证明:![]() 的充要条件是“直线
的充要条件是“直线![]() 的方程为
的方程为![]() ”
”
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com