
| n |
| k-1 |
| n |
| an |
| k |
| k-1 |
| an |
| an-1 |
| k |
| k-1 |
| k |
| k-1 |
| k |
| k-1 |
| k |
| k-1 |
| k |
| k-1 |
| 1 |
| k-1 |
| C | 0n |
| C | 1n |
| 1 |
| k-1 |
| C | 2n |
| 1 |
| k-1 |
| C | nn |
| 1 |
| k-1 |
| n |
| k-1 |
| 1 |
| 2 |
| 2 |
| 22 |
| 3 |
| 23 |
| n |
| 2n |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 22 |
| 2 |
| 23 |
| 3 |
| 24 |
| n |
| 2n+1 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 22 |
| 1 |
| 23 |
| 1 |
| 2n |
| n |
| 2n+1 |
| ||||
1-
|
| n |
| 2n+1 |
| 1 |
| 2n |
| n |
| 2n+1 |
| n+2 |
| 2n |



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
| n |
| k+1 |
| n |
 |
| i=0 |
| a | 2 n-i |
| C | i 2n-i+1 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
 ��2009•����һģ������P��1��0��������C��y=x2��x��0�������ߣ��е�ΪQ1��ûQ1��x���ϵ�ͶӰ��P1���ֹ�P1��������C�����ߣ��е�ΪQ2����Q2��x���ϵ�ͶӰ��P2����������ȥ���õ�һϵ�е�Q1Q2����Qn����Qn�ĺ�����Ϊan��
��2009•����һģ������P��1��0��������C��y=x2��x��0�������ߣ��е�ΪQ1��ûQ1��x���ϵ�ͶӰ��P1���ֹ�P1��������C�����ߣ��е�ΪQ2����Q2��x���ϵ�ͶӰ��P2����������ȥ���õ�һϵ�е�Q1Q2����Qn����Qn�ĺ�����Ϊan��| an | (an-1)(an+1-1) |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
| n | an |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
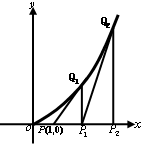 ��2013•�عض�ģ����ͼ������P��1��0��������C��y=x2��x�ʣ�0��+�ޣ��������ߣ��е�ΪQ1�����Q1��x���ϵ�ͶӰ�ǵ�P1���ֹ���P1������C�����ߣ��е�ΪQ2����Q2��x���ϵ�ͶӰ��P2������������ȥ���õ�һϵ�е�Q1��Q2��Q3-Qn�����Qn�ĺ�����Ϊan��
��2013•�عض�ģ����ͼ������P��1��0��������C��y=x2��x�ʣ�0��+�ޣ��������ߣ��е�ΪQ1�����Q1��x���ϵ�ͶӰ�ǵ�P1���ֹ���P1������C�����ߣ��е�ΪQ2����Q2��x���ϵ�ͶӰ��P2������������ȥ���õ�һϵ�е�Q1��Q2��Q3-Qn�����Qn�ĺ�����Ϊan��| 1 |
| d1 |
| 1 |
| d2 |
| 1 |
| dn |
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com