练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】已知数列{an}满足an= ，若从{an}中提取一个公比为q的等比数列{a }，其中k1=1且k1＜k2＜…＜kn ， kn∈N*，则满足条件的最小q的值为（ ）
    A.
    B.
    C.
    D.2

    【答案】D
    【解析】解：∵数列{an}满足an= ，

    ∴ ， ，a4=4， ，

    ， ， ，a10=8，…

    若取q= = ，则 =2× = ≠a3，不在数列{an}中；

    若取q= = ，则 = ，不在数列{an}中；

    若取q= =2，则 =2×22=2×22=8=a10，在数列{an}中．

    综上，满足条件的最小的q的值为2．

    故选：D．

    【考点精析】解答此题的关键在于理解等比数列的通项公式（及其变式）的相关知识，掌握通项公式：．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】已知a，b，c∈R，a2+b2+c2=1．
    （Ⅰ）求证：|a+b+c|≤ ；
    （Ⅱ）若不等式|x﹣1|+|x+1|≥（a+b+c）2对一切实数a，b，c恒成立，求实数x的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设椭圆C： + =1（a＞b＞0），定义椭圆的“伴随圆”方程为x2+y2=a2+b2；若抛物线x2=4y的焦点与椭圆C的一个短轴重合，且椭圆C的离心率为 ．
    （1）求椭圆C的方程和“伴随圆”E的方程；
    （2）过“伴随圆”E上任意一点P作椭圆C的两条切线PA，PB，A，B为切点，延长PA与“伴随圆”E交于点Q，O为坐标原点．
    ①证明：PA⊥PB；
    ②若直线OP，OQ的斜率存在，设其分别为k1 ， k2 ， 试判断k1k2是否为定值，若是，求出该值；若不是，请说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，P（x0 ， y0）是椭圆 +y2=1的上的点，l是椭圆在点P处的切线，O是坐标原点，OQ∥l与椭圆的一个交点是Q，P，Q都在x轴上方

    （1）当P点坐标为（ ， ）时，利用题后定理写出l的方程，并验证l确定是椭圆的切线；
    （2）当点P在第一象限运动时（可以直接应用定理）
    ①求△OPQ的面积
    ②求直线PQ在y轴上的截距的取值范围．
    定理：若点（x0 ， y0）在椭圆 +y2=1上，则椭圆在该点处的切线方程为 +y0y=1．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，在三棱锥S﹣ABC中，SA⊥底面ABC，AC=AB=SA=2，AC⊥AB，D，E分别是AC，BC的中点，F在SE上，且SF=2FE．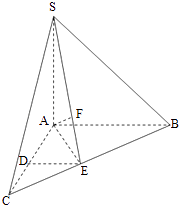
    （1）求证：AF⊥平面SBC；
    （2）在线段上DE上是否存在点G，使二面角G﹣AF﹣E的大小为30°？若存在，求出DG的长；若不存在，请说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图1，在直角梯形ABCD中，AD∥BC，AB⊥BC，BD⊥DC，点E是BC边的中点，将△ABD沿BD折起，使平面ABD⊥平面BCD，连接AE，AC，DE，得到如图2所示的几何体．
    （Ⅰ）求证：AB⊥平面ADC；
    （Ⅱ）若AD=1，二面角C﹣AB﹣D的平面角的正切值为 ，求二面角B﹣AD﹣E的余弦值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】长郡中学早上8点开始上课，若学生小典与小方匀在早上7：40至8：00之间到校，且两人在该时间段的任何时刻到校都是等可能的，则小典比小方至少早5分钟到校的概率为（ ）
    A.
    B.
    C.
    D.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】直线mx+ny=1与圆x2+y2=4的交点为整点（横纵坐标均为正数的点），这样的直线的条数是（ ）
    A.2
    B.4
    C.6
    D.8

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】下列四个判断： ①某校高三一班和高三二班的人数分别是m，n，某次测试数学平均分分别是a，b，则这两个班的数学平均分为 ；
    ②10名工人某天生产同一零件的件数分别是15，17，14，10，15，17，17，16，14，12，设其平均数为a，中位数为b，众数为c，则有c＞a＞b；
    ③从总体中抽取的样本为 ，则回归直线 必过点（ ）
    ④已知ξ服从正态分布N（0，σ2），且P（﹣2≤ξ≤0）=4，则P（ξ＞2）=0.2
    其中正确的个数有（ ）
    A.4个
    B.3个
    C.2个
    D.1个

    查看答案和解析>>

    同步练习册答案