
【题目】几位同学在研究函数![]()
![]() 时,给出了下面几个结论:
时,给出了下面几个结论:
①![]() 的单调减区间是
的单调减区间是![]() ,单调增区间是
,单调增区间是![]() ;
;
②若![]() ,则一定有
,则一定有![]() ;
;
③函数![]() 的值域为
的值域为![]() ;
;
④若规定![]() ,
,![]() ,则
,则![]() 对任意
对任意![]() 恒成立.
恒成立.
上述结论中正确的是____
【答案】②④
【解析】
根据题意,以此分析命题:①可根据函数的解析式判断出其是一个增函数;②由①可得到结果;③函数f(x)的值域为(﹣1,1),可由绝对值不等式的性质证明得;④由其形式知,此是一个与自然数有关的命题,故采用归纳推理的方法证明,即可得答案.
①函数![]() 是一个奇函数,当x≥0时,
是一个奇函数,当x≥0时,![]() ,判断知函数在(0,+∞)上是一个增函数,由奇函数的性质知,函数
,判断知函数在(0,+∞)上是一个增函数,由奇函数的性质知,函数![]() (x∈R)是一个增函数,故若x1≠x2,则一定有f(x1)≠f(x2),此命题①不正确;
(x∈R)是一个增函数,故若x1≠x2,则一定有f(x1)≠f(x2),此命题①不正确;
②由①已证,故此命题正确;
③|x|<1+|x|,故![]()
![]() ,函数f(x)的值域为(﹣1,1),③不正确;
,函数f(x)的值域为(﹣1,1),③不正确;
④当n=1,f1(x)=f(x)=![]() ,
,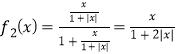 假设n=k时,
假设n=k时,![]() 成立,则n=k+1时,
成立,则n=k+1时,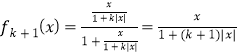 成立,类推可得到,此命题正确.
成立,类推可得到,此命题正确.
故答案为:②④


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】如图是一个几何体的平面展开图,其中四边形ABCD为正方形,△PDC, △PBC, △PAB, △PDA为全等的等边三角形,E、F分别为PA、PD的中点,在此几何体中,下列结论中错误的为 ( )

A. 平面BCD⊥平面PAD B. 直线BE与直线AF是异面直线
C. 直线BE与直线CF共面 D. 面PAD与面PBC的交线与BC平行
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】湖南省某自来水公司每个月(记为一个收费周期)对用户收一次水费,收费标准如下:当每户用水量不超过30吨时,按每吨2元收取;当该用户用水量超过30吨但不超过50吨时,超出部分按每吨3元收取;当该用户用水量超过50吨时,超出部分按每吨4元收取。
(1)记某用户在一个收费周期的用水量为![]() 吨,所缴水费为
吨,所缴水费为![]() 元,写出
元,写出![]() 关于
关于![]() 的函数解析式;
的函数解析式;
(2)在某一个收费周期内,若甲、乙两用户所缴水费的和为214元,且甲、乙两用户用水量之比为3:2,试求出甲、乙两用户在该收费周期内各自的用水量.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图:某污水处理厂要在一个矩形污水处理池(ABCD)的池底水平铺设污水净化管道(Rt△FHE,H是直角顶点)来处理污水,管道越长,污水净化效果越好.设计要求管道的接口H是AB的中点,E,F分别落在线段BC,AD上.已知AB=20米,AD=10 ![]() 米,记∠BHE=θ.
米,记∠BHE=θ. 
(1)试将污水净化管道的长度L表示为θ的函数,并写出定义域;
(2)问:当θ取何值时,污水净化效果最好?并求出此时管道的长度.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() 关于
关于![]() 轴对称,顶点在坐标原点
轴对称,顶点在坐标原点![]() ,直线
,直线![]() 经过抛物线
经过抛物线![]() 的焦点.
的焦点.
(1)求抛物线![]() 的标准方程;
的标准方程;
(2)若不经过坐标原点![]() 的直线
的直线![]() 与抛物线
与抛物线![]() 相交于不同的两点
相交于不同的两点![]() ,
, ![]() ,且满足
,且满足![]() ,证明直线
,证明直线![]() 过
过![]() 轴上一定点
轴上一定点![]() ,并求出点
,并求出点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=(a+2cos2x)cos(2x+θ)为奇函数,且f( ![]() )=0,其中a∈R,θ∈(0,π).
)=0,其中a∈R,θ∈(0,π).
(1)求a,θ的值;
(2)若f( ![]() )=﹣
)=﹣ ![]() ,α∈(
,α∈( ![]() ,π),求sin(α+
,π),求sin(α+ ![]() )的值.
)的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com