
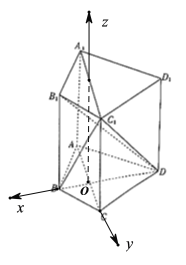
【题目】在四棱柱ABCD﹣A1B1C1D1中,∠BAD=∠BCD=90°,∠ADC=60°且AD=CD,BB1⊥平面ABCD,BB1=2AB=2.
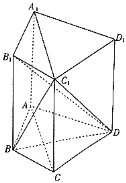
(1)证明:AC⊥B1D.
(2)求BC1与平面B1C1D所成角的正弦值.
【答案】(1)答案见解析.(2)![]()
【解析】
(1)设![]() 相交于
相交于![]() ,通过证明
,通过证明![]() ,证得
,证得![]() ,由此证得
,由此证得![]() ,根据
,根据![]() 平面
平面![]() ,证得
,证得![]() ,由此证得
,由此证得![]() 平面
平面![]() ,进而证得
,进而证得![]() .
.
(2)以![]() 为空间坐标原点建立空间直角坐标系,通过直线
为空间坐标原点建立空间直角坐标系,通过直线![]() 的方向向量和平面
的方向向量和平面![]() 的法向量,求得线面角的正弦值.
的法向量,求得线面角的正弦值.
(1)证明:设AC,BD交于点O,
∵AD=CD,∴∠DAC=∠DCA,
又∠BAD=∠BCD,∴∠BAC=∠BCA,∴AB=AC,
∴△ABD≌△CBD,∴∠ADB=∠CDB,
∴△AOD≌△COD,∴∠AOD=∠COD=90°,
∴AC⊥BD,
又BB1⊥平面ABCD,AC平面ABCD,
∴AC⊥BB1,又BD∩BB1=B,
∴AC⊥平面BDB1,又B1D平面BDB1,
∴AC⊥B1D.
(2)由(1)知![]() ,所以
,所以![]() ,所以
,所以![]() ,所以
,所以![]() .以
.以![]() 为原点建立如图所示的空间直角坐标系
为原点建立如图所示的空间直角坐标系![]() ,则
,则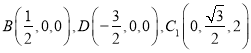 ,
,![]() ,所以
,所以 ,
,![]() ,所以
,所以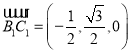 .设平面
.设平面![]() 的法向量为
的法向量为![]() ,则
,则 ,即
,即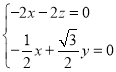 ,令
,令![]() 得
得![]() ,设直线
,设直线![]() 与平面
与平面![]() 所成角为
所成角为![]() ,则
,则
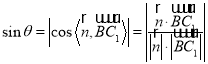
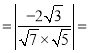
![]() .
.


科目:高中数学 来源: 题型:
【题目】我国古代典籍《周易》用“卦”描述万物的变化,每一卦由六爻组成.其中有一种起卦方法称为“金钱起卦法”,其做法为:取三枚相同的钱币合于双手中,上下摇动数下使钱币翻滚摩擦,再随意抛撒钱币到桌面或平盘等硬物上,如此重复六次,得到六爻.若三枚钱币全部正面向上或全部反面向上,就称为变爻.若每一枚钱币正面向上的概率为![]() ,则一卦中恰有两个变爻的概率为( )
,则一卦中恰有两个变爻的概率为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】足球是当今世界传播范围最广、参与人数最多的体育运动,具有广泛的社会影响,深受世界各国民众喜爱.
(1)为调查大学生喜欢足球是否与性别有关,随机选取50名大学生进行问卷调查,当问卷评分不低于80分则认为喜欢足球,当评分低于80分则认为不喜欢足球,这50名大学生问卷评分的结果用茎叶图表示如图:
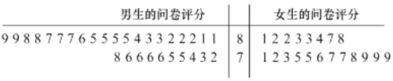
请依据上述数据填写如下列联表:
喜欢足球 | 不喜欢足球 | 总计 | |
女生 |
|
|
|
男生 |
|
|
|
总计 |
|
|
|
请问是否有 ![]() 的把握认为喜欢足球与性别有关?
的把握认为喜欢足球与性别有关?
参考公式及数据: ,
,![]() .
.
| 0.100 | 0.050 | 0.010 | 0.001 |
| 2.706 | 3.841 | 6.635 | 10.828 |
(2)已知某国“糖果盒”足球场每年平均上座率![]() 与该国成年男子国家足球队在国际足联的年度排名
与该国成年男子国家足球队在国际足联的年度排名![]() 线性相关,数据如表
线性相关,数据如表![]() ,
,![]() ,
,![]() ,
,![]()
年度排名 | 9 |
| 6 |
| 3 |
平均上座率 | 0.9 | 0.91 | 0.92 | 0.93 | 0.95 |
求变量![]() 与
与![]() 的线性回归方程
的线性回归方程![]() ,并预测排名为1时该球场的上座率.
,并预测排名为1时该球场的上座率.
参考公式及数据: ,
,![]() ;
;![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本小题满分13分,(Ⅰ)小问5分,(Ⅱ)小问8分.)
甲、乙、丙三人按下面的规则进行乒乓球比赛:第一局由甲、乙参加而丙轮空,以后每一局由前一局的获胜者与轮空者进行比赛,而前一局的失败者轮空.比赛按这种规则一直进行到其中一人连胜两局或打满6局时停止.设在每局中参赛者胜负的概率均为![]() ,且各局胜负相互独立.求:(Ⅰ)打满3局比赛还未停止的概率;(Ⅱ)比赛停止时已打局数
,且各局胜负相互独立.求:(Ⅰ)打满3局比赛还未停止的概率;(Ⅱ)比赛停止时已打局数![]() 的分别列与期望E
的分别列与期望E![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】大学先修课程是在高中开设的具有大学水平的课程,旨在让学有余力的高中生早接受大学思维方式、学习方法的训练,为大学学习乃至未来的职业生涯做好准备.某高中成功开设大学先修课程已有两年,共有![]() 人参与学习先修课程,这两年学习先修课程的学生都参加了高校的自主招生考试(满分
人参与学习先修课程,这两年学习先修课程的学生都参加了高校的自主招生考试(满分![]() 分),结果如下表所示:
分),结果如下表所示:
分数 |
|
|
|
|
|
人数 |
|
|
|
|
|
参加自主招生获得通过的概率 |
|
|
|
|
|
(1)这两年学校共培养出优等生![]() 人,根据图中等高条形图,填写相应列联表,并根据列联表检验能否在犯错的概率不超过
人,根据图中等高条形图,填写相应列联表,并根据列联表检验能否在犯错的概率不超过![]() 的前提下认为学习先修课程与优等生有关系?
的前提下认为学习先修课程与优等生有关系?

优等生 | 非优等生 | 总计 | |
学习大学先修课程 |
| ||
没有学习大学先修课程 | |||
总计 |
|
(2)已知今年全校有![]() 名学生报名学习大学选项课程,并都参加了高校的自主招生考试,以前两年参加大学先修课程学习成绩的频率作为今年参加大学先修课程学习成绩的概率.
名学生报名学习大学选项课程,并都参加了高校的自主招生考试,以前两年参加大学先修课程学习成绩的频率作为今年参加大学先修课程学习成绩的概率.
(i)在今年参与大学先修课程学习的学生中任取一人,求他获得高校自主招生通过的概率;
(ii)某班有![]() 名学生参加了大学先修课程的学习,设获得高校自主招生通过的人数为
名学生参加了大学先修课程的学习,设获得高校自主招生通过的人数为![]() ,求
,求![]() 的分布列和数学期望.
的分布列和数学期望.
参考数据:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
参考公式: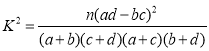 ,其中
,其中![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数).在以坐标原点为极点,
为参数).在以坐标原点为极点,![]() 轴正半轴为极轴的极坐标系中,曲线
轴正半轴为极轴的极坐标系中,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)写出![]() 的普通方程和
的普通方程和![]() 的直角坐标方程;
的直角坐标方程;
(2)若![]() 与
与![]() 相交于
相交于![]()
![]() 两点,求
两点,求![]() 的面积.
的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在统计调查中,问卷的设计是一门很大的学问,特别是对一些敏感性问题.例如学生在考试中有无作弊现象,社会上的偷税漏税等.更要精心设计问卷.设法消除被调查者的顾虑,使他们能够如实回答问题,否则被调查者往往会拒绝冋答,或不提供真实情况,为了调查中学生中的早恋现象,随机抽出300名学生,调查中使用了两个问題.①你的学籍号的最后一位数是奇数(学籍号的后四位是序号);②你是否有早恋现象,让被调查者从装有4个红球,6个黑球(除颜色外完全相同)的袋子中随机摸取两个球.摸到两球同色的学生如实回答第一个问题,摸到两球异色的学生如实回答第二个问题,回答“是”的人往一个盒子中放一个小石子,回答“否”的人什么都不放,后来在盒子中收到了78个小石子.
(1)你能否估算出中学生早恋人数的百分比?
(2)若从该地区中学生中随机抽取一个班(40人),设其中恰有![]() 个人存在早恋的现象,求
个人存在早恋的现象,求![]() 的分布列及数学期望.
的分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某农业观光区的平面示意图如图所示,其中矩形![]() 的长
的长![]() 千米,宽
千米,宽![]() 千米,半圆的圆心
千米,半圆的圆心![]() 为
为![]() 中点,为了便于游客观光休闲,在观光区铺设一条由圆弧
中点,为了便于游客观光休闲,在观光区铺设一条由圆弧![]() 、线段
、线段![]() 、
、![]() 组成的观光道路,其中线段
组成的观光道路,其中线段![]() 经过圆心
经过圆心![]() ,点
,点![]() 在线段
在线段![]() 上(不含线段端点
上(不含线段端点![]() 、
、![]() ),已知道路
),已知道路![]() 、
、![]() 的造价为每千米
的造价为每千米![]() 万元,道路
万元,道路![]() 造价为每千米
造价为每千米![]() 万元,设
万元,设![]() ,观光道路的总造价为
,观光道路的总造价为![]() .
.

(1)试求![]() 与
与![]() 的函数关系式
的函数关系式![]() ,并写出
,并写出![]() 的取值范围;
的取值范围;
(2)当![]() 为何值时,观光道路的总造价
为何值时,观光道路的总造价![]() 最小.
最小.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com