
 +2
+2 +1
+1 +1)2
+1)2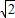 +2
+2 ,代入xy=1+x+y中,转化为关于x+y的一元二次不等式,进而求得x+y的最小值,同理求得xy的最小值,即可得到答案.
,代入xy=1+x+y中,转化为关于x+y的一元二次不等式,进而求得x+y的最小值,同理求得xy的最小值,即可得到答案. (当且仅当x=y时成立).
(当且仅当x=y时成立). ,解得x+y≥2+2
,解得x+y≥2+2 或x+y≤2-2
或x+y≤2-2 (舍),A符合题意,可排除C;
(舍),A符合题意,可排除C;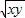 (当且仅当x=y时成立),
(当且仅当x=y时成立), ≥1+
≥1+ 或
或 ≤1-
≤1- (舍),即xy≥3+2
(舍),即xy≥3+2 从而排除B,D.
从而排除B,D.

 夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com