
【题目】某物流公司购买了一块长AM=30米,宽AN=20米的矩形地块,计划把图中矩形ABCD建设为仓库,其余地方为道路和停车场,要求顶点C在地块对角线MN上,B、D分别在边AM、AN上,假设AB的长度为x米
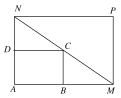
(1)求矩形ABCD的面积S关于x的函数解析式;
(2)要使仓库占地ABCD的面积不少于144平方米,则AB的长度应在什么范围内?
 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案科目:高中数学 来源: 题型:
【题目】已知△ABC的三边所在直线的方程分别是lAB:4x-3y+10=0,lBC:y=2,lCA:3x-4y=5.
(1)求∠BAC的平分线所在直线的方程;
(2)求AB边上的高所在直线的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工厂生产甲、乙两种产品.已知生产一吨甲产品、一吨乙产品所需要的煤、电以及产值如表所示;又知道国家每天分配给该厂的煤和电力有限制,每天供煤至多56吨,供电至多45千瓦.问该厂如何安排生产,才能使该厂日产值最大?最大的产值是多少?
用煤(吨) | 用电(千瓦) | 产值(万元) | |
生产一吨 甲种产品 | 7 | 2 | 8 |
生产一吨 乙种产品 | 3 | 5 | 11 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,PD垂直正方形ABCD所在平面,AB=2,E是PB的中点, ![]() ,
, ![]() >
>![]() .
.

(1)建立适当的空间坐标系,求出点E的坐标;
(2)在平面PAD内求一点F,使EF⊥平面PCB.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设数列{an}的前n项和为Sn . 若对n∈N* , 总k∈N* , 使得Sn=ak , 则称数列{an}是“G数列”. (Ⅰ)若数列{an}是等差数列,其首项a1=1,公差d=﹣1.证明:数列{an}是“G数列”;
(Ⅱ)若数列{an}的前n项和Sn=3n(n∈N*),判断数列{an}是否为“G数列”,并说明理由;
(Ⅲ)证明:对任意的等差数列{an},总存在两个“G数列”{bn}和{cn},使得an=bn+cn(n∈N*)成立.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知△ABC中A,B,C所对的边分别为a,b,c, ![]() (1﹣cos2B)=8sinBsinC,A+
(1﹣cos2B)=8sinBsinC,A+ ![]() =π.
=π.
(Ⅰ)求cosB的值;
(Ⅱ)若点D在线段BC上,且BD=6,c=5,求△ADC的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com