
【题目】已知函数f(x)=(x﹣a)2lnx(a为常数).
(1)若f(x)在(1,f(1))处的切线与直线2x+2y﹣3=0垂直.
(ⅰ)求实数a的值;
(ⅱ)若a非正,比较f(x)与x(x﹣1)的大小;
(2)如果0<a<1,判断f(x)在(a,1)上是否有极值,若有极值是极大值还是极小值?若无极值,请说明理由.
【答案】
(1)解:(ⅰ)f(x)定义域是(0,+∞),f′(x)=(x﹣a)(2lnx+ ![]() ),
),
∵直线2x+2y﹣3=0的斜率为:k=﹣1,
∴f(x)在(1,f(1))处的切线的斜率﹣ ![]() =1,
=1,
即f′(1)=(1﹣a)(2ln1+ ![]() )=(1﹣a)2=1,
)=(1﹣a)2=1,
∴a=0或a=2;
(ⅱ)由(ⅰ)知,a=0,∴f(x)=x2lnx,
∵x2lnx﹣x(x﹣1)=x(xlnx﹣x+1),
∴令g(x)=xlnx﹣x+1,g′(x)=lnx,
当x>1时,g′(x)>0,当0<x<1时,g′(x)<0,
∴g(x)在(0,1)单调递减,在(1,+∞)单调递增,
g(x)min=g(1)=0,∴g(x)≥0恒成立,
即f(x)≥x(x﹣1);
(2)解:f′(x)=(x﹣a)(2lnx+ ![]() ),
),
令F(x)=2lnx+1﹣ ![]() ,F′(x)=
,F′(x)= ![]() >0,
>0,
∴F(x)在(a,1)上单调递增,又F(1)=1﹣a>0,F(a)=2lna<0,
所以在(a,1)上必存在x0,使F(x0)=0,
又x﹣a>0,∴当x∈(a,x0),f′(x)<0,x∈(x0,1),f′(x)>0,
∴f(x)在(a,x0)单调递减,在(x0,1)单调递增,
∴x=x0是f(x)的极值点,且为极小值.
【解析】(1)(i)求出f(x)的导数,根据切线的斜率是f′(1)=﹣ ![]() =1,解出a的值即可;(ii)求出f(x)的表达式,作差,得到x2lnx﹣x(x﹣1)=x(xlnx﹣x+1),令g(x)=xlnx﹣x+1,根据函数的单调性求出g(x)的最小值g(1)=0,得到g(x)≥0恒成立,从而求出f(x)与x(x﹣1)的大小即可;(2)求出f′(x)=(x﹣a)(2lnx+
=1,解出a的值即可;(ii)求出f(x)的表达式,作差,得到x2lnx﹣x(x﹣1)=x(xlnx﹣x+1),令g(x)=xlnx﹣x+1,根据函数的单调性求出g(x)的最小值g(1)=0,得到g(x)≥0恒成立,从而求出f(x)与x(x﹣1)的大小即可;(2)求出f′(x)=(x﹣a)(2lnx+ ![]() ),令F(x)=2lnx+1﹣
),令F(x)=2lnx+1﹣ ![]() ,求出F(x)的导数,根据函数的单调性求出函数的极值即可.
,求出F(x)的导数,根据函数的单调性求出函数的极值即可.
【考点精析】利用函数的极值与导数对题目进行判断即可得到答案,需要熟知求函数![]() 的极值的方法是:(1)如果在
的极值的方法是:(1)如果在![]() 附近的左侧
附近的左侧![]() ,右侧
,右侧![]() ,那么
,那么![]() 是极大值(2)如果在
是极大值(2)如果在![]() 附近的左侧
附近的左侧![]() ,右侧
,右侧![]() ,那么
,那么![]() 是极小值.
是极小值.


 寒假乐园北京教育出版社系列答案
寒假乐园北京教育出版社系列答案科目:高中数学 来源: 题型:
【题目】已知全集为实数集R,集合A={x|y= ![]() +
+ ![]() },B={x|2x>4}
},B={x|2x>4}
( I)分别求A∪B,A∩B,(UB)∪A
( II)已知集合C={x|1<x<a},若CA,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
已知圆的参数方程为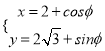 (
(![]() 为参数),以直角坐标系的原点为极点,
为参数),以直角坐标系的原点为极点, ![]() 轴的非负半轴为极轴,建立极坐标系,直线
轴的非负半轴为极轴,建立极坐标系,直线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(Ⅰ)将圆的参数方程化为普通方程,再化为极坐标方程;
(Ⅱ)若点![]() 在直线
在直线![]() 上,当点
上,当点![]() 到圆的距离最小时,求点
到圆的距离最小时,求点![]() 的极坐标.
的极坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数y=x+ ![]() 有如下性质:如果常数t>0,那么该函数在
有如下性质:如果常数t>0,那么该函数在 ![]() 上是减函数,在
上是减函数,在 ![]() 上是增函数.
上是增函数.
(1)已知f(x)= ![]() ,x∈[﹣1,1],利用上述性质,求函数f(x)的单调区间和值域;
,x∈[﹣1,1],利用上述性质,求函数f(x)的单调区间和值域;
(2)对于(1)中的函数f(x)和函数g(x)=﹣x﹣2a,若对任意x1∈[﹣1,1],总存在x2∈[0,1],使得g(x2)=f(x1)成立,求实数a的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在直三棱柱A1B1C1﹣ABC中,AB⊥AC,AB=AC=2,AA1=4,点D是BC的中点. 
(1)求证:A1B∥平面ADC1;
(2)求平面ADC1与ABA1所成二面角的平面角的正弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com