
思路解析:(1)要求k的值,必须建立关于k的方程,由已知OA⊥OB,所以kOA·kOB=-1,及A、B既在直线上,又在双曲线上可得k的值.(2)为开放性题目,一般方法为:假设存在,根据已知求解,若解出而且符合题意则存在,若无解或解出不符合题意,则不存在.
解:(1)设A(x1,kx1+1),B(x2,kx2+1),则以AB为直径的圆过原点的充要条件是(![]() )·(
)·(![]() )=-1,
)=-1,
即(k2+1)x1x2+k(x1+x2)+1=0. ①
由方程组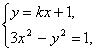 消去y,得(3-k2)x2-2kx-2=0. ②
消去y,得(3-k2)x2-2kx-2=0. ②
∴x1+x2=![]() ,x1x2=
,x1x2=![]() ,代入①得
,代入①得![]() +
+![]() +1=0,
+1=0,
解得k2=1,∴k=1或k=-1,当k=1时,方程②为2x2-2x-2=0,有两个不等实根;当k=-1时,方程②为x2+x-1=0,有两个不等实根,故k=±1时,以AB为直径的圆过原点.
(2)若A(x1,kx1+1),B(x2,kx2+1)关于y=2x对称,
则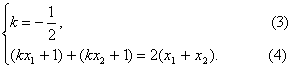
④整理得(k-2)(x1+x2)+2=0.
∵x1+x2=![]() ,∴
,∴![]() +2=0,解得k=
+2=0,解得k=![]() .
.
这个结果与③矛盾,故不存在k的值,使A、B两点关于直线y=2x对称.


 经典密卷系列答案
经典密卷系列答案 金牌课堂练系列答案
金牌课堂练系列答案 三新快车金牌周周练系列答案
三新快车金牌周周练系列答案科目:高中数学 来源: 题型:
| x2 |
| 2 |
| y2 |
| m |
| A、(1,2] |
| B、[1,2) |
| C、[1,2)∪[2,+∞) |
| D、(2,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
| x2 |
| a2 |
| y2 |
| b2 |
| ||
| 2 |
4
| ||
| 5 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com