
【题目】如图,在矩形ABCD中,AB=2BC,点M在边DC上,点F在边AB上,且DF⊥AM,垂足为E,若将△ADM沿AM折起,使点D位于D′位置,连接D′B,D′C得四棱锥D′﹣ABCM. 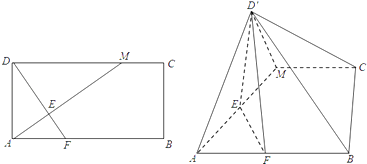
(1)求证:AM⊥D′F;
(2)若∠D′EF= ![]() ,直线D'F与平面ABCM所成角的大小为
,直线D'F与平面ABCM所成角的大小为 ![]() ,求直线AD′与平面ABCM所成角的正弦值.
,求直线AD′与平面ABCM所成角的正弦值.
【答案】
(1)证明:∵AM⊥D′E,AM⊥EF,D′E∩⊥EF=E,
∴AM⊥面D′EF
∵D′F面D′EF,
∴AM⊥D′F;
(2)解:由(1)知,AM⊥面D′EF,AM平面ABCM,
∴平面ABCM⊥面D′EF,
∴过D′作D′H⊥EF,则D′H⊥平面ABCM,
∴∠D′FH也就是∠D′FE是直线D'F与平面ABCM所成角,由已知,∠D′FE= ![]() ,
,
并且∠D′AH是所求的直线AD′与平面ABCM所成角.
∵∠D′EF= ![]() ,且∠D′FE=
,且∠D′FE= ![]()
在三角形△D′EF中,∵∠D′EF= ![]() ,且∠D′FE=
,且∠D′FE= ![]()
所以是等边三角形,∴D′E=EF,即DE=EF,∴△DAF是等腰三角形.
设AD=2,∴AF=2,EF= ![]() ,四棱锥D′﹣ABCM的高D′H=
,四棱锥D′﹣ABCM的高D′H= ![]()
由于直线AD′与平面ABCM所成角为∠D′AH,∴sin∠D′AH= ![]() =
= ![]()

【解析】(1)根据图形折叠前后的关系,易证AM⊥面D′EF,得出AM⊥D′F.(2)由(1)知,AM⊥面D′EF,所以平面ABCM⊥面D′EF,过D′作D′H⊥EF,则D′H⊥平面ABCM,,∠D′FH是直线D'F与平面ABCM所成角,∠D′AH是直线AD′与平面ABCM所成角在直角三角形D′AH求解即可.
【考点精析】根据题目的已知条件,利用直线与平面垂直的性质和空间角的异面直线所成的角的相关知识可以得到问题的答案,需要掌握垂直于同一个平面的两条直线平行;已知![]() 为两异面直线,A,C与B,D分别是
为两异面直线,A,C与B,D分别是![]() 上的任意两点,
上的任意两点,![]() 所成的角为
所成的角为![]() ,则
,则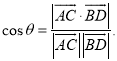 .
.


 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案科目:高中数学 来源: 题型:
【题目】函数g(x)=log2 ![]() (x>0),关于方程|g(x)|2+m|g(x)|+2m+3=0有三个不同实数解,则实数m的取值范围为( )
(x>0),关于方程|g(x)|2+m|g(x)|+2m+3=0有三个不同实数解,则实数m的取值范围为( )
A.(﹣∞,4﹣2 ![]() )∪(4
)∪(4 ![]() ,+∞)
,+∞)
B.(4﹣2 ![]() ,4
,4 ![]() )
)
C.(﹣ ![]() ,﹣
,﹣ ![]() )
)
D.(﹣ ![]() ,﹣
,﹣ ![]() ]
]
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数y=f(x)对任意x∈R,恒有(f(x)﹣sinx)(f(x)﹣cosx)=0成立,则下列关于函数 y=f(x)的说法正确的是( )
A.最小正周期是2π
B.值域是[﹣1,1]
C.是奇函数或是偶函数
D.以上都不对
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】求满足下列各条件的椭圆的标准方程.
(1)长轴长是短轴长的2倍且经过点A(2,0);
(2)短轴一个端点与两焦点组成一个正三角形,且焦点到同侧顶点的距离为.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=alnx﹣x2+1.
(Ⅰ)若曲线y=f(x)在x=1处的切线方程为4x﹣y+b=0,求实数a和b的值;
(Ⅱ)讨论函数f(x)的单调性;
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com