
【题目】已知椭圆![]() 的顶点
的顶点![]() 到左焦点
到左焦点![]() 的距离为
的距离为![]() ,离心率
,离心率![]() .
.

(1)求椭圆![]() 的方程;
的方程;
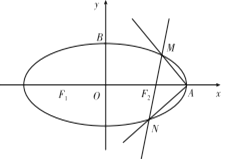
(2)若点![]() 为椭圆
为椭圆![]() 的右頂点,过点
的右頂点,过点![]() 作互相垂直的两条射线,与椭圆
作互相垂直的两条射线,与椭圆![]() 分別交于不同的两点
分別交于不同的两点![]() 不与左、右顶点重合) ,试判断直线
不与左、右顶点重合) ,试判断直线![]() 是否过定点,若过定点,求出该定点的坐标;若不过定点,请说明理由.
是否过定点,若过定点,求出该定点的坐标;若不过定点,请说明理由.
【答案】(1)![]() ;(2)直线过定点
;(2)直线过定点![]() .
.
【解析】
试题分析:(1)根据题意列出![]() 的方程组结合
的方程组结合![]() ,求出
,求出![]() 的值;(2)当直线
的值;(2)当直线![]() 的斜率不存在时,求出
的斜率不存在时,求出![]() 两点坐标,可得其与
两点坐标,可得其与![]() 的交点,当当直线的斜率存在时,设直线
的交点,当当直线的斜率存在时,设直线![]() 的方程为
的方程为![]() ,整理方程组可得
,整理方程组可得![]() 两点坐标的关系,根据
两点坐标的关系,根据![]() 及椭圆的右顶点
及椭圆的右顶点![]()
![]() ,由向量的数量积坐标表示出
,由向量的数量积坐标表示出![]() 的关系,代入直线方程即可求得直线经过的定点.
的关系,代入直线方程即可求得直线经过的定点.
试题解析:(1)由题意可知: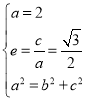 , 解得:
, 解得:![]() ,故椭圆的标准方程为
,故椭圆的标准方程为![]() .
.
(2)设![]() 当直线
当直线![]() 的斜率不存在时,
的斜率不存在时,![]() 轴,
轴,![]() 为等腰直角三角形,
为等腰直角三角形,
![]() ,又
,又![]() ,又
,又![]() 不与左、右顶点重合,解得
不与左、右顶点重合,解得![]() ,此时,直线
,此时,直线![]() 过点
过点![]() .
.
当直线的斜率存在时,设直线![]() 的方程为
的方程为![]() ,由方程组
,由方程组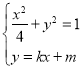 ,得
,得![]() ,整理得
,整理得![]() ,则
,则![]() .由已知
.由已知![]() ,且椭圆的右顶点
,且椭圆的右顶点![]() 为
为![]() ,所以
,所以![]() ,
,![]() ,即
,即![]() ,整理得
,整理得![]() ,解得
,解得![]() 或
或![]() 均满足
均满足![]() 成立.当
成立.当![]() 时,直线
时,直线![]() 的方程
的方程![]() 过顶点
过顶点![]() ,与题意矛盾舍去.当
,与题意矛盾舍去.当![]() 时,直线
时,直线![]() 的方程
的方程![]() 过定点
过定点![]() ,故直线过定点,且定点是
,故直线过定点,且定点是![]() .
.


 特高级教师点拨系列答案
特高级教师点拨系列答案科目:高中数学 来源: 题型:
【题目】选修4-1:几何证明选讲
如图所示,已知圆![]() 外有一点
外有一点![]() ,作圆
,作圆![]() 的切线
的切线![]() ,
,![]() 为切点,过
为切点,过![]() 的中点
的中点![]() ,作割线
,作割线![]() ,交圆于
,交圆于![]() 、
、![]() 两点,连接
两点,连接![]() 并延长,交圆
并延长,交圆![]() 于点
于点![]() ,连接
,连接![]() 交圆
交圆![]() 于点
于点![]() ,若
,若![]() .
.

(Ⅰ)求证:![]() ;
;
(Ⅱ)求证:四边形![]() 是平行四边形.
是平行四边形.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】脱贫是政府关注民生的重要任务,了解居民的实际收入状况就显得尤为重要.现从某地区随机抽取![]() 个农户,考察每个农户的年收入与年积蓄的情况进行分析,设第
个农户,考察每个农户的年收入与年积蓄的情况进行分析,设第![]() 个农户的年收入
个农户的年收入![]() (万元),年积蓄
(万元),年积蓄![]() (万元),经过数据处理得
(万元),经过数据处理得![]()
(Ⅰ)已知家庭的年结余![]() 对年收入
对年收入![]() 具有线性相关关系,求线性回归方程;
具有线性相关关系,求线性回归方程;
(Ⅱ)若该地区的农户年积蓄在![]() 万以上,即称该农户已达小康生活,请预测农户达到小康生活的最低年收入应为多少万元?
万以上,即称该农户已达小康生活,请预测农户达到小康生活的最低年收入应为多少万元?
附:在![]() 中,
中, 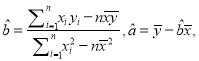 其中
其中![]() 为样本平均值.
为样本平均值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校高二某班的一次数学测试成绩的茎叶图和频率分布直方图都受到不同程度的损坏,可见部分如下:

试着根据表中的信息解答下列问题:
(Ⅰ)求全班的学生人数及分数在[70,80)之间的频数;
(Ⅱ)为快速了解学生的答题情况,老师按分层抽样的方法从位于[70,80)和[80,90)分数段的试卷中抽取7份进行分析,再从中任选2人进行交流,求交流的学生中,成绩位于[70,80)分数的人恰有一人被抽到的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】海州市英才中学某兴趣小组欲研究昼夜温差大小与患感冒人数多少之间的关系,他们分別到气象局与某医院抄录了![]() 至
至![]() 月份每月
月份每月![]() 号的昼夜温差情况与因患感冒而就诊的人数,得到如下资料(表):
号的昼夜温差情况与因患感冒而就诊的人数,得到如下资料(表):
日期 |
|
|
|
|
|
|
昼夜温差 |
|
|
|
|
|
|
就诊人数 |
|
|
|
|
|
|
该兴趣小组确定的研究方案是:先从这六组数据中选取![]() 组,用剩下的
组,用剩下的![]() 组数据求线性回归方程,再用被选取的
组数据求线性回归方程,再用被选取的![]() 组数据进行检验.
组数据进行检验.
(1)求选取的![]() 组数据恰好是相邻两个月的概率;
组数据恰好是相邻两个月的概率;
(2)若选取的是![]() 月与6月的两组数据,请根据
月与6月的两组数据,请根据![]() 至
至![]() 月份的数据,求出
月份的数据,求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ;
;
(3)若由线性回归方程得到的估计数据与所选出的检验数据的误差均不超过![]() 人,则认为得到的线性回归方程是理想的,试问该小组所得线性回归方程是否理想.
人,则认为得到的线性回归方程是理想的,试问该小组所得线性回归方程是否理想.
其中回归系数公式, ,
,![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校的一个社会实践调查小组,在对该校学生的良好“用眼习惯”的调查中,随机发放了120分问卷.对收回的100份有效问卷进行统计,得到如![]() 下列联表:
下列联表:
做不到科学用眼 | 能做到科学用眼 | 合计 | |
男 | 45 | 10 | 55 |
女 | 30 | 15 | 45 |
合计 | 75 | 25 | 100 |
(1)现按女生是否能做到科学用眼进行分层,从45份女生问卷中抽取了6份问卷,从这6份问卷中再随机抽取3份,并记其中能做到科学用眼的问卷的份数![]() ,试求随机变量
,试求随机变量![]() 的分布列和数学期望;
的分布列和数学期望;
(2)若在犯错误的概率不超过![]() 的前提下认为良好“用眼习惯”与性别有关,那么根据临界值表,最精确的
的前提下认为良好“用眼习惯”与性别有关,那么根据临界值表,最精确的![]() 的值应为多少?请说明理由.
的值应为多少?请说明理由.
附:独立性检验统计量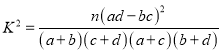 ,其中
,其中![]() .
.
独立性检验临界值表:
| 0.25 | 0.15 | 0.10 | 0.05 | 0.025 |
| 1.323 | 2.072 | 2.706 | 3.840 | 5.024 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
已知曲线C的极坐标方程是![]() ,以极点为平面直角坐标系的原点,极轴为x轴的正半轴,建立平面直角坐标系,直线L的参数方程是
,以极点为平面直角坐标系的原点,极轴为x轴的正半轴,建立平面直角坐标系,直线L的参数方程是 (t为参数).
(t为参数).
(1)求曲线C的直角坐标方程和直线L的普通方程;
(2)设点P(m,0),若直线L与曲线C交于两点A,B,且![]() ,求实数m的值.
,求实数m的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某烟花厂家为了测试最新研制出的一种“冲天”产品升空的安全性,特对其进行了一项测试。如图,这种烟花在燃放点C进行燃放实验,测试人员甲、乙分别在A,B两地(假设三地在同一水平面上),测试人员甲测得A、B两地相距80米且∠BAC=60°,甲听到烟花燃放“冲天”时的声音的时间比乙晚![]() 秒.在A地测得该烟花升至最高点H处的仰角为60°.(已知声音的传播速度为340米∕秒)
秒.在A地测得该烟花升至最高点H处的仰角为60°.(已知声音的传播速度为340米∕秒)
(1)求甲距燃放点C的距离;(2)求这种烟花的垂直“冲天”高度HC

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com