
【题目】如图,在平面四边形ABCD中,已知A=![]() ,B=
,B=![]() ,AB=6.在AB边上取点E,使得BE=1,连接EC,ED.若∠CED=
,AB=6.在AB边上取点E,使得BE=1,连接EC,ED.若∠CED=![]() ,EC=
,EC=![]() .
.

(1)求sin∠BCE的值;
(2)求CD的长.
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,直线
中,直线![]() 的参数方程
的参数方程![]() (
(![]() 为参数),以坐标原点为极点,
为参数),以坐标原点为极点, ![]() 轴正半轴为极轴建立极坐标系,曲线
轴正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为:
的极坐标方程为: ![]() .
.
(1)把直线![]() 的参数方程化为极坐标方程,把曲线
的参数方程化为极坐标方程,把曲线![]() 的极坐标方程化为普通方程;
的极坐标方程化为普通方程;
(2)求直线![]() 与曲线
与曲线![]() 交点的极坐标(
交点的极坐标(![]() ≥0,0≤
≥0,0≤![]() ).
).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆![]() 关于直线
关于直线![]() 对称的圆为
对称的圆为![]() .
.
(1)求圆C的方程;
(2)过点(1,0)作直线l与圆C交于A,B两点,O是坐标原点,是否存在直线l,使得∠AOB=90°?若存在,求出所有满足条件的直线l的方程;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】椭圆![]() :
:![]()
![]() 的离心率为
的离心率为![]() ,抛物线
,抛物线![]() :
:![]() 截
截![]() 轴所得的线段长等于
轴所得的线段长等于![]() .
.![]() 与
与![]() 轴的交点为
轴的交点为![]() ,过点
,过点![]() 作直线
作直线![]() 与
与![]() 相交于点
相交于点![]() 直线
直线![]() 分别与
分别与![]() 相交于
相交于![]() .
.
(1)求证:![]() ;
;
(2)设![]() ,
,![]() 的面积分别为
的面积分别为![]() ,若
,若![]()
![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,一个铝合金窗分为上、下两栏,四周框架和中间隔档的材料为铝合金,宽均为6![]() ,上栏与下栏的框内高度(不含铝合金部分)的比为1:2,此铝合金窗占用的墙面面积为28800
,上栏与下栏的框内高度(不含铝合金部分)的比为1:2,此铝合金窗占用的墙面面积为28800![]() ,设该铝合金窗的宽和高分别为
,设该铝合金窗的宽和高分别为![]() ,铝合金窗的透光部分的面积为
,铝合金窗的透光部分的面积为![]() .
.
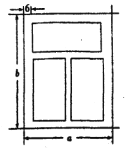
(1)试用![]() 表示
表示![]() ;
;
(2)若要使![]() 最大,则铝合金窗的宽和高分别为多少?
最大,则铝合金窗的宽和高分别为多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某地区某农产品近几年的产量统计如表:
年份 | 2013 | 2014 | 2015 | 2016 | 2017 | 2018 |
年份代码 | 1 | 2 | 3 | 4 | 5 | 6 |
年产量 | 6.6 | 6.7 | 7 | 7.1 | 7.2 | 7.4 |
(1)根据表中数据,建立![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ;
;
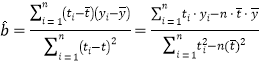 ,
,![]()
(2)若近几年该农产品每千克的价格![]() (单位:元)与年产量
(单位:元)与年产量![]() 满足的函数关系式为
满足的函数关系式为![]() ,且每年该农产品都能售完.
,且每年该农产品都能售完.
①根据(1)中所建立的回归方程预测该地区2019(![]() )年该农产品的产量;
)年该农产品的产量;
②当![]() 为何值时,销售额
为何值时,销售额![]() 最大?
最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市为了制定合理的节水方案,对居民用水情况进行了调查,通过抽样,获得了某年100位居民每人的月均用水量(单位:吨),将数据按照[0,0.5),[0.5,1),[4,4.5]分成9组,制成了如图所示的频率分布直方图.
(I)求直方图中的a值;
(II)设该市有30万居民,估计全市居民中月均用水量不低于3吨的人数,说明理由。

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com