
【题目】在如图所示的六面体中,面![]() 是边长为2的正方形,面
是边长为2的正方形,面![]() 是直角梯形,
是直角梯形,![]() ,
,![]() .
.
(1)求证:![]() 平面
平面![]() ;
;
(2)若二面角![]() 为60°,求直线
为60°,求直线![]() 和平面
和平面![]() 所成角的正弦值.
所成角的正弦值.
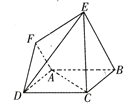
【答案】(1)证明见解析;(2)![]() .
.
【解析】试题分析:(1)连接![]() 相交于点
相交于点![]() ,取
,取![]() 的中点为
的中点为![]() ,连接
,连接![]() ,易证四边形
,易证四边形![]() 是平行四边形,从而可得结论;(2)以
是平行四边形,从而可得结论;(2)以![]() 为坐标原点,
为坐标原点,![]() 为
为![]() 轴、
轴、![]() 为
为![]() 轴、
轴、![]() 为
为![]() 轴建立空间直角坐标系.则
轴建立空间直角坐标系.则![]() ,计算法向量,根据公式
,计算法向量,根据公式![]() 即可求出.
即可求出.
试题解析:
(1):连接![]() 相交于点
相交于点![]() ,取
,取![]() 的中点为
的中点为![]() ,连接
,连接![]() .
.
![]() 是正方形,
是正方形,![]() 是
是![]() 的中点,
的中点,![]() ,
,
又因为![]() ,所以
,所以![]() 且
且![]() ,
,
所以四边形![]() 是平行四边形,
是平行四边形,
![]() ,又因为
,又因为![]() 平面
平面![]() 平面
平面![]()
![]() 平面
平面![]()
(2)![]() 是正方形,
是正方形,![]() 是直角梯形,
是直角梯形,![]() ,
,
![]()
![]() ,
,![]() 平面
平面![]() ,同理可得
,同理可得![]() 平面
平面![]() .
.
又![]() 平面
平面![]() ,所以平面
,所以平面![]() 平面
平面![]() ,
,
又因为二面角![]() 为60°,
为60°,
所以![]() ,由余弦定理得
,由余弦定理得![]() ,
,
所以![]() ,因为
,因为![]() 半面
半面![]() ,
,
![]() ,所以
,所以![]() 平面
平面![]() ,
,
以![]() 为坐标原点,
为坐标原点,![]() 为
为![]() 轴、
轴、![]() 为
为![]() 轴、
轴、![]() 为
为![]() 轴建立空间直角坐标系.
轴建立空间直角坐标系.
则![]() ,
,
所以![]() ,
,
设平面![]() 的一个法向量为
的一个法向量为![]() ,
,
则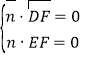 即
即![]() 令
令![]() ,则
,则![]() ,
,
所以![]()
设直线![]() 和平面
和平面![]() 所成角为
所成角为![]() ,
,
则![]()



科目:高中数学 来源: 题型:
【题目】已知圆![]() 有以下性质:
有以下性质:
①过圆![]() 上一点
上一点![]() 的圆的切线方程是
的圆的切线方程是![]() .
.
②若不在坐标轴上的点![]() 为圆
为圆![]() 外一点,过
外一点,过![]() 作圆
作圆![]() 的两条切线,切点分别为
的两条切线,切点分别为![]() ,则
,则![]() 垂直
垂直![]() ,即
,即![]() .
.
(1)类比上述有关结论,猜想过椭圆![]() 上一点
上一点![]() 的切线方程 (不要求证明);
的切线方程 (不要求证明);
(2)若过椭圆![]() 外一点
外一点![]() (
(![]() 不在坐标轴上)作两直线,与椭圆相切于
不在坐标轴上)作两直线,与椭圆相切于![]() 两点,求证:
两点,求证:![]() 为定值.
为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2019年是中华人民共和国成立70周年,某校党支部举办了一场“我和我的祖国”知识竞赛,满分100分,回收40份答卷,成绩均落在区间![]() 内,将成绩绘制成如下的频率分布直方图.
内,将成绩绘制成如下的频率分布直方图.
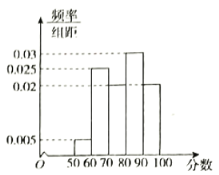
(1)估计知识竞赛成绩的中位数和平均数;
(2)从![]() ,
,![]() 分数段中,按分层抽样随机抽取5份答卷,再从对应的党员中选出3位党员参加县级交流会,求选出的3位党员中有2位成绩来自于
分数段中,按分层抽样随机抽取5份答卷,再从对应的党员中选出3位党员参加县级交流会,求选出的3位党员中有2位成绩来自于![]() 分数段的概率.
分数段的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设椭圆 ![]() 的左右顶点分别为A,B,点P在椭圆上且异于A,B两点,O为坐标原点.
的左右顶点分别为A,B,点P在椭圆上且异于A,B两点,O为坐标原点.
(1)若直线AP与BP的斜率之积为 ![]() ,求椭圆的离心率;
,求椭圆的离心率;
(2)若|AP|=|OA|,证明直线OP的斜率k满足|k|> ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】首届中国国际进口博览会在2018年11月5日—10日在上海国家会展中心举办。会议期间,某公司欲采购东南亚某水果种植基地的水果,公司刘总经理与该种植基地的负责人陈老板商定一次性采购一种水果的采购价![]() (元/吨)与采购量
(元/吨)与采购量![]() (吨)之间的函数关系的图象如图中的折线
(吨)之间的函数关系的图象如图中的折线![]() 所示(不包含端点
所示(不包含端点![]() ,但包含端点
,但包含端点![]() ).
).

(Ⅰ)求![]() 与
与![]() 之间的函数关系式;
之间的函数关系式;
(Ⅱ)已知该水果种植基地种植该水果的成本是2800元/吨,那么刘总经理的采购量为多少时,该水果基地在这次买卖中所获得利润![]() 最大?最大利润是多少?
最大?最大利润是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司生产甲、乙两种产品所得利润分别为![]() 和
和![]() (万元),它们与投入资金(万元)的关系有经验公式
(万元),它们与投入资金(万元)的关系有经验公式![]() ,
,![]() .今将120万元资金投入生产甲、乙两种产品,并要求对甲、乙两种产品的投资金额都不低于20万元.
.今将120万元资金投入生产甲、乙两种产品,并要求对甲、乙两种产品的投资金额都不低于20万元.
(Ⅰ)设对乙产品投入资金![]() 万元,求总利润
万元,求总利润![]() (万元)关于
(万元)关于![]() 的函数关系式及其定义域;
的函数关系式及其定义域;
(Ⅱ)如何分配使用资金,才能使所得总利润最大?最大利润为多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在梯形![]() 中,
中, ![]() ,
, ![]() ,
, ![]() ,四边形
,四边形![]() 为矩形,平面
为矩形,平面![]() 平面
平面![]() ,
, ![]() .
.

(Ⅰ)求证: ![]() 平面
平面![]() ;
;
(Ⅱ)点![]() 在线段
在线段![]() 上运动,设平面
上运动,设平面![]() 与平面
与平面![]() 所成锐二面角为
所成锐二面角为![]() ,试求
,试求![]() 的最小值.
的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com