
【题目】已知△ABC的三个内角A、B、C的对边分别为a、b、c,且b2+c2=a2+bc,求:
(1)2sinBcosC﹣sin(B﹣C)的值;
(2)若a=2,求△ABC周长的最大值.
【答案】
(1)解:∵b2+c2=a2+bc,∴a2=b2+c2﹣bc,
结合余弦定理知cosA= ![]() =
= ![]() =
= ![]() ,
,
又A∈(0,π),∴A= ![]() ,
,
∴2sinBcosC﹣sin(B﹣C)=sinBcosC+cosBsinC
=sin(B+C)=sin[π﹣A]=sinA= ![]()
(2)解:由a=2,结合正弦定理得:
![]() =
= ![]() =
= ![]() ,
,
∴b= ![]() sinB,c=
sinB,c= ![]() sinC,
sinC,
则a+b+c=2+ ![]() sinB+
sinB+ ![]() sinC
sinC
=2+ ![]() sinB+
sinB+ ![]() sin(
sin( ![]() ﹣B)
﹣B)
=2+2 ![]() sinB+2cosB=2+4sin(B+
sinB+2cosB=2+4sin(B+ ![]() ),
),
可知周长的最大值为6
【解析】(1)根据余弦定理表示出cosA,把已知得等式变形后代入即可求出cosA的值,由A的范围,利用特殊角的三角函数值即可求出A的度数,然后把所求的式子利用两角和与差的正弦函数公式及诱导公式化简,将sinA的值代入即可求出值;(2)由a=2和sinA的值,根据正弦定理表示出b和c,代入三角形的周长a+b+c中,利用两角和与差的正弦函数公式及特殊角的三角函数值化为一个角的正弦函数,根据正弦函数的值域即可得到周长的最大值.


科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
: ![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,其离心率
,其离心率![]() ,以原点为圆心,椭圆的半焦距为半径的圆与直线
,以原点为圆心,椭圆的半焦距为半径的圆与直线![]() 相切.
相切.
(1)求![]() 的方程;
的方程;
(2)过![]() 的直线
的直线![]() 交
交![]() 于
于![]() 两点,
两点, ![]() 为
为![]() 的中点,连接
的中点,连接![]() 并延长交
并延长交![]() 于点
于点![]() ,若四边形
,若四边形![]() 的面积
的面积![]() 满足:
满足: ![]() ,求直线
,求直线![]() 的斜率.
的斜率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知P为△ABC内一点,且满足 ![]() ,记△ABP,△BCP,△ACP的面积依次为S1 , S2 , S3 , 则S1:S2:S3等于( )
,记△ABP,△BCP,△ACP的面积依次为S1 , S2 , S3 , 则S1:S2:S3等于( )
A.1:2:3
B.1:4:9
C.2:3:1
D.3:1:2
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,直三棱柱![]() 中,各棱长均为6,
中,各棱长均为6, ![]() 分别是侧棱
分别是侧棱![]() 、
、![]() 上的点,且
上的点,且![]() .
.
(1)在![]() 上是否存在一点
上是否存在一点![]() ,使得
,使得![]() 平面
平面![]() ?证明你的结论;
?证明你的结论;
(2)求异面直线![]() 与
与![]() 所成角的余弦值.
所成角的余弦值.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线L:kx-y+1+2k=0.
(1)求证:直线L过定点;
(2)若直线L交x轴负半轴于点A,交y正半轴于点B,△AOB的面积为S,试求S的最小值并求出此时直线L的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2016年被业界称为![]() (虚拟现实技术)元年,未来
(虚拟现实技术)元年,未来![]() 技术将给教育、医疗、娱乐、商业、交通旅游等多领域带来极大改变,某
技术将给教育、医疗、娱乐、商业、交通旅游等多领域带来极大改变,某![]() 教育设备生产企业有甲、乙两类产品,其中生产一件甲产品需
教育设备生产企业有甲、乙两类产品,其中生产一件甲产品需![]() 团队投入15天时间,
团队投入15天时间, ![]() 团队投入20天时间,总费用10万元,甲产品售价为15万元/件;生产一件乙产品需
团队投入20天时间,总费用10万元,甲产品售价为15万元/件;生产一件乙产品需![]() 团队投入20天时间,
团队投入20天时间, ![]() 团队投入16天时间,总费用15万元,乙产品售价为25万元/件,
团队投入16天时间,总费用15万元,乙产品售价为25万元/件, ![]() 、
、![]() 两个团队分别独立运作.现某客户欲以不超过200万元订购该企业甲、乙两类产品,要求每类产品至少各3件,在期限180天内,为使企业总效益最佳,则最后交付的甲、乙两类产品数之和为__________.
两个团队分别独立运作.现某客户欲以不超过200万元订购该企业甲、乙两类产品,要求每类产品至少各3件,在期限180天内,为使企业总效益最佳,则最后交付的甲、乙两类产品数之和为__________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(12分)在△ABC中,角A,B,C所对的边分别为a,b,c,已知cosC+(cosA﹣![]() sinA)cosB=0.
sinA)cosB=0.
(1)求角B的大小; (2)若a+c=1,求b的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某地随着经济的发展,居民收入逐年增长,下表是该地一建设银行连续五年的储蓄存款(年底余额),如下表1:
年份x | 2011 | 2012 | 2013 | 2014 | 2015 |
储蓄存款y(千亿元) | 5 | 6 | 7 | 8 | 10 |
为了研究计算的方便,工作人员将上表的数据进行了处理, ![]() 得到下表2:
得到下表2:
时间代号t | 1 | 2 | 3 | 4 | 5 |
z | 0 | 1 | 2 | 3 | 5 |
(Ⅰ)求z关于t的线性回归方程;
(Ⅱ)通过(Ⅰ)中的方程,求出y关于x的回归方程;
(Ⅲ)用所求回归方程预测到2020年年底,该地储蓄存款额可达多少?
(附:对于线性回归方程![]() ,其中
,其中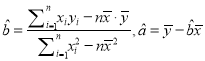 )
)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com