
【题目】已知定义在R上的函数y=f(x)满足:①对于任意的x∈R,都有f(x+2)=f(x﹣2);②函数y=f(x+2)是偶函数;③当x∈(0,2]时,f(x)=ex﹣ ![]() ,a=f(﹣5),b=f(
,a=f(﹣5),b=f( ![]() ).c=f(
).c=f( ![]() ),则a,b,c的大小关系是( )
),则a,b,c的大小关系是( )
A.a<b<c
B.c<a<b
C.c<a<b
D.b<a<c
科目:高中数学 来源: 题型:
【题目】在△ABC中,角A,B,C所对的边分别为a,b,c,且满足csinA=acosC
(1)求角C大小;
(2)求 ![]() sinA﹣cos(B+
sinA﹣cos(B+ ![]() )的最大值,并求取得最大值时角A,B的大小.
)的最大值,并求取得最大值时角A,B的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=lnx﹣x2与g(x)=(x﹣2)2﹣ ![]() ﹣m的图象上存在关于(1,0)对称的点,则实数m的取值范围是( )
﹣m的图象上存在关于(1,0)对称的点,则实数m的取值范围是( )
A.(﹣∞,1﹣ln2)
B.(﹣∞,1﹣ln2]
C.(1﹣ln2,+∞)
D.[1﹣ln2,+∞)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥ABCD﹣A1B1C1D1中,底面ABCD是等腰梯形,AB∥CD,AB=2,BC=CD=1,顶角D1在底面ABCD内的射影恰好为点C. 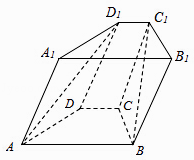
(1)求证:AD1⊥BC;
(2)若直线DD1与直线AB所成角为 ![]() ,求平面ABC1D1与平面ABCD所成角(锐角)的余弦值函数值.
,求平面ABC1D1与平面ABCD所成角(锐角)的余弦值函数值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在某次试验中,有两个试验数据![]() ,统计的结果如下面的表格1.
,统计的结果如下面的表格1.
(1)在给出的坐标系中画出![]() 的散点图; 并判断正负相关;
的散点图; 并判断正负相关;
(2)填写表格2,然后根据表格2的内容和公式求出![]() 对
对![]() 的回归直线方程
的回归直线方程![]() ,并估计当
,并估计当![]() 为10时
为10时![]() 的值是多少?(公式:
的值是多少?(公式: ,
,![]() )
)
| 1 | 2 | 3 | 4 | 5 |
| 2 | 3 | 4 | 4 | 5 |
表1

表格2
序号 | | | | |
1 | 1 | 2 | ||
2 | 2 | 3 | ||
3 | 3 | 4 | ||
4 | 4 | 4 | ||
5 | 5 | 5 | ||
|
|
|
|
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】阅读如图所示的程序框图,则该算法的功能是( ) 
A.计算数列{2n﹣1}前5项的和
B.计算数列{2n﹣1}前6项的和
C.计算数列{2n﹣1}前5项的和
D.计算数列{2n﹣1}前6项的和
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=  ,若存在实数x1 , x2 , x3 , x4满足f(x1)=f(x2)=f(x3)=f(x4),其中x1<x2<x3<x4 , 则x1x2x3x4取值范围是( )
,若存在实数x1 , x2 , x3 , x4满足f(x1)=f(x2)=f(x3)=f(x4),其中x1<x2<x3<x4 , 则x1x2x3x4取值范围是( )
A.(60,96)
B.(45,72)
C.(30,48)
D.(15,24)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}的各项都是正数,a1=1,an+12=an2+ ![]() (n∈N*)
(n∈N*)
(1)求证: ![]() ≤an<2(n≥2)
≤an<2(n≥2)
(2)求证:12(a2﹣a1)+22(a3﹣a2)+…+n2(an+1﹣an)> ![]() ﹣
﹣ ![]() (n∈N*)
(n∈N*)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com