
����Ŀ����ij��λ��ְ��ʳ���У�ʳ��ÿ����3Ԫ/���ļ۸������깺�������Ȼ����5Ԫ/���ļ۸���ۣ�������������꣬ʣ�µ������1Ԫ/���ļ۸��������ϼӹ�������������ͳ�����ϣ��õ�ʳ��ÿ�������������Ƶ�ʷֲ�ֱ��ͼ����ͼ��ʾ��ʳ��ij�칺����90���������x����λ������60��x��110����ʾ�������������T����λ��Ԫ����ʾ����
������T����x�ĺ�������ʽ��
������ֱ��ͼ��������T������100Ԫ�ĸ��ʣ�
������ֱ��ͼ�������������У��Ը���������е�ֵ��������ĸ���ֵ����������������������Ƶ����Ϊ������ȡ�������м�ֵ�ĸ��ʣ����磺��������x��[60��70������ȡx=65����x=65�ĸ��ʵ�������������[60��70����Ƶ�ʣ�����T�ķֲ��к���ѧ������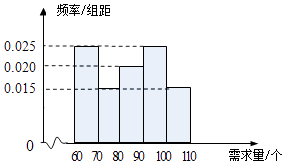
���𰸡��⣺���������⣬��60��X��90ʱ������T=5X+1����90��X����3��90=4X��180�� ��90��X��110ʱ������T=5��90��3��90=180��
��T����x�ĺ�������ʽT=  ��
��
���������⣬������T������100ԪΪ�¼�A��
�ɣ���֪������T������100Ԫʱ����4X��180��100��
��X��70����70��X��110��
��ֱ��ͼ��֪����70��X��110ʱ��
���������
P��A��=1��P�� ![]() ��=1��0.025����70��60��=0.75��
��=1��0.025����70��60��=0.75��
���������⣬����4��65��180=80��4��75��180=120��
4��85��180=160��
������T��ȡֵ��Ϊ��80��120��160��180��
��P��T=80��=0.25��P��T=120��=0.15��P��T=160��=0.2��P��T=180��=0.4������9�֣�
��T�ķֲ���Ϊ��
T | 80 | 120 | 160 | 180 |
P | 0.25 | 0.15 | 0.2 | 0.4 |
���������ѧ������
E��T��=80��0.25+120��0.15+160��0.20+180��0.40=142
�����������������⣬��60��X��90ʱ���������T����90��X��110ʱ���������T���ɴ������T����x�ĺ�������ʽ�����������⣬������T������100ԪΪ�¼�A������T������100Ԫʱ����70��X��110���ɴ����ö����¼����ʼ��㹫ʽ�����T�ķֲ��к���ѧ��������III�������⣬����T��ȡֵ��Ϊ��80��120��160��180���ֱ������Ӧ�ĸ��ʣ��ɴ�������������ѧ����E��T����
�����㾫����ͨ�����������ɢ�������������ֲ��У��������������Ʒ����������У������������X����ȡ��ֵ�����ǿ���һ������һһ�г����������������������ɢ�������������ɢ����������ķֲ��У�һ���,����ɢ���������X����ȡ��ֵΪx1,x2,.....,xi,......,xn��Xȡÿһ��ֵ xi(i=1,2,......���ĸ���P(��=xi����Pi����Ʊ�Ϊ��ɢ���������X �ĸ��ʷֲ�����Ʒֲ��м����Խ����⣮


 ��У����ϵ�д�
��У����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���Ȳ�����{an}�У�Sn��ǰn��ͣ���S3=S8 �� S7=Sk �� ��k��ֵΪ�� ��
A.4
B.11
C.2
D.12
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����к����������ڣ����ޣ�0���ϵ����ݼ���ż�����ǣ� ��
A.![]()
B.y=|log2����x��|
C.![]()
D.y=sin|x|
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪������R�ϵ��溯��f��x������f��x+2��=��f��x������x��[0��1]ʱ��f��x��=2x��1���� ��
A.![]()
B.![]()
C.![]()
D.![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����f��x��=m��|x��2|��m��R����f��x+2����0�Ľ⼯Ϊ[��3��3]��
���ⲻ��ʽ��f��x��+f��x+2����0��
������a��b��c��Ϊ��ʵ����������a+b+c=m����֤�� ![]() ��3��
��3��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ֱ������ϵxoy�У���֪��P��0�� ![]() ��������C�IJ�������Ϊ
��������C�IJ�������Ϊ ![]() ����Ϊ����������ԭ��Ϊ���㣬x��������Ϊ���Ὠ��������ϵ��ֱ��l�ļ����귽��Ϊ��=
����Ϊ����������ԭ��Ϊ���㣬x��������Ϊ���Ὠ��������ϵ��ֱ��l�ļ����귽��Ϊ��= ![]() ��
��
�����жϵ�P��ֱ��l��λ�ù�ϵ��˵�����ɣ�
������ֱ��l������C����������ֱ�ΪA��B���� ![]() ��ֵ��
��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ڡ�ABC�У�a��b��c�ֱ��ǽ�A��B��C�ĶԱߣ���8sin2 ![]() ��
��
��1�����A�Ĵ�С��
��2����a= ![]() ��b+c=3����b��c��ֵ��
��b+c=3����b��c��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪�Ȳ�����{an}��a1=��ll������d��0����a2 �� a5 �� a6�ɵȱ����У�
��1��������{an}��ͨ�ʽ��
��2����bn=|an|��������{bn}��ǰn���Tn ��
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com