
【题目】如图,直三棱柱![]() 中,
中,![]() ,
,![]() ,
, ![]() ,外接球的球心为
,外接球的球心为![]() ,点
,点![]() 是侧棱
是侧棱![]() 上的一个动点.有下列判断:
上的一个动点.有下列判断:
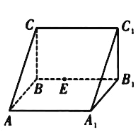
① 直线![]() 与直线
与直线![]() 是异面直线;②
是异面直线;②![]() 一定不垂直
一定不垂直![]() ;
;
③ 三棱锥![]() 的体积为定值; ④
的体积为定值; ④![]() 的最小值为
的最小值为![]() .
.
其中正确的序号序号是______.
【答案】①③④
【解析】
由题意画出图形,由异面直线的概念判断①;利用线面垂直的判定与性质判断②;找出球心,由棱锥底面积与高为定值判断③;设BE=x,列出AE+EC1关于x的函数式,结合其几何意义求出最小值判断④.
如图,
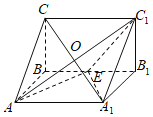
∵直线AC经过平面BCC1B1内的点C,而直线C1E在平面BCC1B1内不过C,
∴直线AC与直线C1E是异面直线,故①正确;
当E与B重合时,AB1⊥A1B,而C1B1⊥A1B,
∴A1B⊥平面AB1C1,则A1E垂直AC1,故②错误;
由题意知,直三棱柱ABC﹣A1B1C1的外接球的球心为O是AC1 与A1C 的交点,则△AA1O的面积为定值,由BB1∥平面AA1C1C,
∴E到平面AA1O的距离为定值,∴三棱锥E﹣AA1O的体积为定值,故③正确;
设BE=x,则B1E=2﹣x,∴AE+EC1![]() .
.
由其几何意义,即平面内动点(x,1)与两定点(0,0),(2,0)距离和的最小值知,
其最小值为2![]() ,故④正确.
,故④正确.
故答案为:①③④


科目:高中数学 来源: 题型:
【题目】设有编号为1,2,3,4,5的五把锁和对应的五把钥匙.现给这5把钥匙也贴上编号为1,2,3,4,5的五个标签,则共有______种不同的贴标签的方法:若想使这5把钥匙中至少有2把能打开贴有相同标签的锁,则有______种不同的贴标签的方法.(本题两个空均用数字作答)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x3![]() ax2﹣x+1(a∈R).
ax2﹣x+1(a∈R).
(1)当a=2时,求曲线y=f(x)在点(1,f (1))处的切线方程;
(2)当a<0时,设g(x)=f(x)+x.
①求函数g(x)的极值;
②若函数g(x)在[1,2]上的最小值是﹣9,求实数a的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】户外运动已经成为一种时尚运动,某单位为了了解员工喜欢户外运动是否与性别有关,决定从本单位全体650人中采用分层抽样的办法抽取50人进行问卷调查,得到了如下列联表:
喜欢户外运动 | 不喜欢户外运动 | 总计 | |
男性 | 5 | ||
女性 | 10 | ||
总计 | 50 |
已知在这50人中随机抽取1人,抽到喜欢户外运动的员工的概率是![]() .
.
(1)请将上面的列联表补充完整;
(2)求该公司男、女员工各多少人;
(3)在犯错误的概率不超过0.005的前提下能否认为喜欢户外运动与性别有关?并说明你的理由.
下面的临界值表仅供参考:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
(参考公式: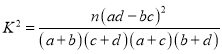 ,其中
,其中![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在如图所示的几何体中,四边形![]() 是正方形,
是正方形,![]() 平面
平面![]() ,
,![]() ,
,![]() 分别是线段
分别是线段![]() ,
,![]() 的中点,
的中点,![]() .
.

(I)在棱![]() 上找一点
上找一点![]() ,使得平面
,使得平面![]() 平面
平面![]() ,请写出点的位置,并加以证明;
,请写出点的位置,并加以证明;
(Ⅱ)求点![]() 到平面
到平面![]() 的距离.
的距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在四棱锥 P - ABCD 中,锐角三角形 PAD 所在平面垂直于平面 PAB,AB⊥AD,AB⊥BC。

(1) 求证:BC∥平面 PAD;
(2) 平面 PAD⊥ 平面 ABCD.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本小题满分12分)如图,曲线![]() 由上半椭圆
由上半椭圆![]() 和部分抛物线
和部分抛物线![]()
![]() 连接而成,
连接而成, ![]() 的公共点为
的公共点为![]() ,其中
,其中![]() 的离心率为
的离心率为![]() .
.
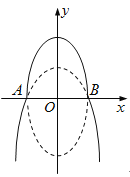
(Ⅰ)求![]() 的值;
的值;
(Ⅱ)过点![]() 的直线
的直线![]() 与
与![]() 分别交于
分别交于![]() (均异于点
(均异于点![]() ),若
),若![]() ,求直线
,求直线![]() 的方程.
的方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com