
【题目】已知函数f(x)=x3-3mx+n(m>0)的极大值为6,极小值为2.
(1)求实数m,n的值;
(2)求f(x)在区间[0,3]上的最大值和最小值.
科目:高中数学 来源: 题型:
【题目】从1到9这9个数字中取3个偶数和4个奇数,试问:
(1)能组成多少个没有重复数字的七位数?
(2)在(1)中的七位数中,偶数排在一起,奇数也排在一起的有多少个?
(3)在(1)中任意2个偶数都不相邻的七位数有多少个?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,直线
中,直线![]() 的直角坐标方程为:
的直角坐标方程为:![]() ,曲线
,曲线![]() 的方程为
的方程为![]() ,现建立以
,现建立以![]() 为极点,
为极点,![]() 轴的正半轴为极轴的极坐标系.
轴的正半轴为极轴的极坐标系.
(1)写出直线![]() 极坐标方程,曲线
极坐标方程,曲线![]() 的参数方程;
的参数方程;
(2)过点![]() 平行于直线
平行于直线![]() 的直线与曲线
的直线与曲线![]() 交于
交于![]() 、
、![]() 两点,若
两点,若![]() ,求点
,求点![]() 轨迹的直角坐标方程.
轨迹的直角坐标方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公园准备在一圆形水池里设置两个观景喷泉,观景喷泉的示意图如图所示,A,B两点为喷泉,圆心O为AB的中点,其中OA=OB=a米,半径OC=10米,市民可位于水池边缘任意一点C处观赏. 
(1)若当∠OBC= ![]() 时,sin∠BCO=
时,sin∠BCO= ![]() ,求此时a的值;
,求此时a的值;
(2)设y=CA2+CB2 , 且CA2+CB2≤232.
(i)试将y表示为a的函数,并求出a的取值范围;
(ii)若同时要求市民在水池边缘任意一点C处观赏喷泉时,观赏角度∠ACB的最大值不小于 ![]() ,试求A,B两处喷泉间距离的最小值.
,试求A,B两处喷泉间距离的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在直三棱柱ABC﹣A1B1C1中,已知AB⊥AC,AB=2,AC=4,AA1=3.D是线段BC的中点. 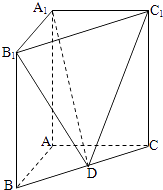
(1)求直线DB1与平面A1C1D所成角的正弦值;
(2)求二面角B1﹣A1D﹣C1的大小的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若正整数N除以正整数m后的余数为n,则记为N≡n(mod m),例如10≡4(mod 6).下面程序框图的算法源于我国古代闻名中外的(中国剩余定理),执行该程序框图,则输出的n等于( ) 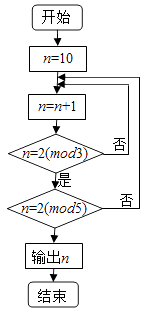
A.17
B.16
C.15
D.13
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某茶楼有四类茶饮,假设为顾客准备泡茶工具所需的时间互相独立,且都是整数分钟,经统计以往为100位顾客准备泡茶工具所需的时间(t),结果如下:
类别 | 铁观音 | 龙井 | 金骏眉 | 大红袍 |
顾客数(人) | 20 | 30 | 40 | 10 |
时间t(分钟/人) | 2 | 3 | 4 | 6 |
注:服务员在准备泡茶工具时的间隔时间忽略不计,并将频率视为概率.
(1)求服务员恰好在第6分钟开始准备第三位顾客的泡茶工具的概率;
(2)用X表示至第4分钟末已准备好了工具的顾客人数,求X的分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某电视台举办青年歌手大奖赛,有十名评委打分,已知甲、乙两名选手演唱后的得分如茎叶图如图所示.
(1)从统计学的角度,你认为甲与乙比较,演唱水平怎样?
(2)现场有三名点评嘉宾A,B,C,每位选手可以从中选两位接受其指导,若选手选每位点评嘉宾的可能性相等,求甲、乙两名选手选择的点评嘉宾恰有一人重复的概率.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com