
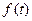 (万人)与时间
(万人)与时间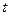 (天)的函数关系近似满足
(天)的函数关系近似满足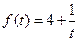 ,人均消费
,人均消费 (元)与时间
(元)与时间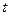 (天)的函数关系近似满足
(天)的函数关系近似满足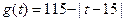 .(Ⅰ)求该城市的旅游日收益
.(Ⅰ)求该城市的旅游日收益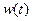 (万元)与时间
(万元)与时间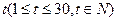 的函数关系式;(Ⅱ)求该城市旅游日收益的最小值(万元).
的函数关系式;(Ⅱ)求该城市旅游日收益的最小值(万元). 科目:高中数学 来源:不详 题型:解答题
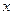 元/千克,政府补贴为
元/千克,政府补贴为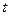 元/千克.根据市场调查,当
元/千克.根据市场调查,当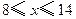 时,淡水鱼的市场日供产量
时,淡水鱼的市场日供产量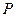 千克与市场日需求量
千克与市场日需求量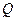 千克近似地满足关系:
千克近似地满足关系: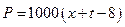 ,
,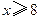 ,
,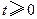 ,
,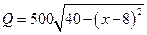 ,
,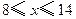 .
.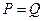 时的市场价格称为市场平衡价格.
时的市场价格称为市场平衡价格.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
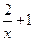 )=lgx,求f(x);
)=lgx,求f(x);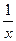 )=3x,求f(x).
)=3x,求f(x).查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 ABP面积为S.(1)求函数S=f(x)的解析式、定义域和值域;(2)求f[f(3)]的值。
ABP面积为S.(1)求函数S=f(x)的解析式、定义域和值域;(2)求f[f(3)]的值。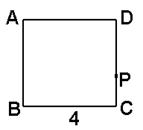
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com