
分析 (1)先根据抛物线方程得到焦点坐标和交点坐标,代入双曲线,把$\frac{p}{2}$=c代入整理得 c4-6a2c2+a4=0等式两边同除以a4,得到关于离心率e的方程,进而可求得e.
(2)先求出M的坐标,由$\overrightarrow{M{F_2}}=4\overrightarrow{N{F_2}}$,求得N的坐标,把N的坐标代入双曲线方程化简求得离心率 e 的大小.
(3)要使直线与双曲线有两个交点,需使双曲线的其中一渐近线方程的斜率小于直线的斜率,即$\frac{b}{a}$<tan30°=$\frac{\sqrt{3}}{3}$,求得a和b的不等式关系,进而转化成a和c的不等式关系,求得离心率的一个范围,最后根据双曲线的离心率大于1,综合可得求得e的范围.
(4)利用离心率的范围进而求得a和c不等式关系,进而利用a,b和c的关系求得a和b的不等式关系,进而求得渐近线斜率k的范围,利用k=tan$\frac{θ}{2}$确定tan$\frac{θ}{2}$的范围,进而确定θ的范围.
解答 解:(1)由题意,∵两条曲线交点的连线过点F
∴两条曲线交点为($\frac{p}{2}$,p),
代入双曲线方程得$\frac{\frac{{p}^{2}}{4}}{{a}^{2}}-\frac{{p}^{2}}{{b}^{2}}$=1,
又$\frac{p}{2}$=c
代入化简得 c4-6a2c2+a4=0
∴e4-6e2+1=0
∴e2=3+2$\sqrt{2}$=(1+$\sqrt{2}$)2
∴e=$\sqrt{2}$+1;
(2)线段F2M所在直线的斜率为 tan60°=$\sqrt{3}$,方程为y-0=$\sqrt{3}$(x-c),
∴M(0,-$\sqrt{3}$c).
设N (m,n ),则
∵$\overrightarrow{M{F_2}}=4\overrightarrow{N{F_2}}$,
∴(c,$\sqrt{3}$c)=4(c-m,-n),
∴c=4c-4m,$\sqrt{3}$c=-4n,∴m=$\frac{3c}{4}$,n=-$\frac{\sqrt{3}}{4}$c,∴N($\frac{3c}{4}$,-$\frac{\sqrt{3}}{4}$c),
把N的坐标代入双曲线方程$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1$,整理得9c4-28a2c2+16a4=0,
∴9e4-28e2+16=0,
∵e>1,∴e2=($\frac{\sqrt{13}+1}{3}$)2,∴e=$\frac{\sqrt{13}+1}{3}$;
(3)要使直线与双曲线有两个交点,需使双曲线的其中一渐近线方程的斜率小于直线的斜率,即$\frac{b}{a}$<tan30°=$\frac{\sqrt{3}}{3}$,∴b<$\frac{\sqrt{3}}{3}$a
∵$\sqrt{{c}^{2}-{a}^{2}}$<$\frac{\sqrt{3}}{3}$a,
整理得e<$\frac{2\sqrt{3}}{3}$
∵双曲线中e>1,∴e的范围是(1,$\frac{2\sqrt{3}}{3}$);
(4)根据定义e=$\frac{\sqrt{{a}^{2}+{b}^{2}}}{a}$,
∵e∈[$\sqrt{2}$,2].
∴$\frac{\sqrt{3}}{3}$b≤a≤b
而渐近线的斜率k=$\frac{b}{a}$,∴1≤k≤$\sqrt{3}$
所以45°≤$\frac{θ}{2}$≤60°
所以 90°≤θ≤120°,即[$\frac{π}{2}$,$\frac{2π}{3}$].
点评 本题考查由圆锥曲线的方程求焦点、考查双曲线的三参数的关系:c2=a2+b2注意与椭圆的区别.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ${y_1}=\frac{(x+3)(x-5)}{x+3},{y_2}=x-5$ | B. | y1=$\sqrt{x+1}$•$\sqrt{x-1}$,y2=$\sqrt{(x+1)(x-1)}$ | ||
| C. | y1=x,y2=$\sqrt{{x}^{2}}$ | D. | y1=$\root{3}{{x}^{4}-{x}^{3}}$,y2=$x\root{3}{x-1}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1023 | B. | 1025 | C. | 513 | D. | 511 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
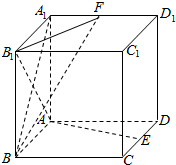 如图,在正方体ABCD-A1B1C1D1中,E、F分别是CD、A1D1中点.
如图,在正方体ABCD-A1B1C1D1中,E、F分别是CD、A1D1中点.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com