
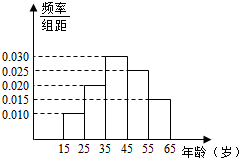
 ij����̨Ϊ�������ϣ�����Ժ���15��65�����Ⱥ��ȡ��n�ˣ��ش����⡰������·�������ļ������У���ͳ�ƽ����ͼ����ʾ��
ij����̨Ϊ�������ϣ�����Ժ���15��65�����Ⱥ��ȡ��n�ˣ��ش����⡰������·�������ļ������У���ͳ�ƽ����ͼ����ʾ��| ��� | ���� | �ش���ȷ������ | �ش���ȷ������ռ�����Ƶ�� |
| ��1�� | [15��25�� | a | 0.5 |
| ��2�� | [25��35�� | 18 | x |
| ��3�� | [35��45�� | b | 0.9 |
| ��4�� | [45��55�� | 9 | 0.36 |
| ��5�� | [55��65�� | 3 | y |
���� ��1������Ƶ�ʱ����������n��ֵ���ٷֱ����a��b��x��y��ֵ��
��2�����÷ֲ�����������2��3��4��ֱ��ȡ��������
��3�������оٷ������6���г�2�˵Ļ����¼����Լ�����ȡ������ǡ��û�е�3���˻����¼����������Ӧ�ĸ���ֵ��
��� �⣺��1����Ƶ�ʱ��е�4�����ݿ�֪����4��������Ϊ$\frac{9}{0.36}$=25��
���Ƶ�ʷֲ�ֱ��ͼ��֪n=$\frac{25}{0.025��10}$=100��
��a=100��0.01��10��0.5=5��
b=100��0.03��10��0.9=27��
�ڶ�������Ϊ0.020��100��10=20��
��5��������0.015��10��100=15
��x=$\frac{18}{20}$=0.9��y=$\frac{3}{15}$=0.2������4�֣�
��2����2��3��4��ش���ȷ�Ĺ���54�ˣ�
�����÷ֲ������54���г�ȡ6�ˣ�ÿ��ֱ��ȡ������Ϊ��
��2�飺$\frac{6}{54}$��18=2���ˣ�����3�飺$\frac{6}{54}$��27=3���ˣ���
��4�飺$\frac{6}{54}$��9=1���ˣ�����8��
��3��������ȡ�����е�2���2��ΪA1��A2��
��3���3��ΪB1��B2��B3����4���1��ΪC1��
���6���г�2�����п��ܵĽ����
��A1��A2������A1��B1������A1��B2������A1��B3������A1��C1����
��A2��B1������A2��B2������A2��B3������A2��C1������B1��B2����
��B1��B3������B1��C1������B2��B3������B2��C1������B3��C1����
��15�������¼�������ǡ��û�е�3���˹�3�������¼���
������ȡ������ǡ��û�е�3���˵ĸ���Ϊ$\frac{3}{15}$=$\frac{1}{5}$������12�֣�
���� ���⿼����Ƶ�ʷֲ�ֱ��ͼ��Ӧ�����⣬Ҳ���������оٷ���ŵ���͵ĸ��ʵ�Ӧ�����⣬���ۺ�����Ŀ��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | -$\frac{1}{2}$ | B�� | 1 | C�� | -$\frac{1}{2}$��1 | D�� | -1��$\frac{1}{2}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 0 | B�� | 1 | C�� | $\sqrt{2}$ | D�� | 2 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | y=$��\frac{5}{4}$x | B�� | y=$��\frac{4}{5}$x | C�� | y=$��\frac{3}{4}$x | D�� | y=$��\frac{4}{3}$x |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 1 | B�� | 1��2 | C�� | 0 | D�� | -1��1��2 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com